Question

【题目】如图,抛物线与x轴交于A(3，0)，B两点，与y轴交于点C，点M(，5)是抛物线上一点,抛物线与抛物线关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′

（1）求抛物线C1的解析式；

（2）过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在，请求出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】（1） （2）P(2,0)或(,0)

【解析】(1)、将点A和点M的坐标代入，利用待定系数法求出函数解析式；(2)、根据函数解析式求出点B和点C的坐标，然后利用轴对称性得出点M′、点A′和点B′的坐标，从而得出直线A′C的直线解析式，根据勾股定理分别求出AC和DA′的长度，设P（m，0），分和两种情况分别求出m的值，得出点P的坐标．

(1)、把A（-3，0），M（，5）代入y=ax2+bx+4得：，

解得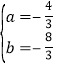：， 所以抛物线C1的解析式为，

(2)、令y=0，则， 解得x1=-3，x2=1， ∴B（1，0），
令x=0，则y=4，∴C（0，4）．由题意，知M′（，5），B′（-1，0），A′（3，0），∠CAA′=∠CA′A，∴AB′=2．设直线A′C的解析式为y=px+q．

把A′（3，0），C（0，4）代入得：，解得：，∴y=，

当x=时，y==2，∴D(，2） 由勾股定理得，AC=5， DA′=．

设P（m，0）． 当m＜3时，此时点P在点A′的左边， 若，即有△DA′P∽△CAB′，

∴， 解得m=2， ∴P（2，0）；

若，即有△DA′P∽△B′AC，∴， 解得m=，∴P(，0)；

当m＞3时，此时点P在点A′的右边，∵∠CB′O≠∠DA′E， ∴∠AB′C≠∠DA′P，

∴此情况，△DA′P与△B′AC不能相似．

综上所述，存在点P（2，0）或(，0)满足条件．