
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(3,0),B两点,与y轴交于点C,点M(
与x轴交于A(3,0),B两点,与y轴交于点C,点M(![]() ,5)是抛物线
,5)是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 与抛物线
与抛物线![]() 关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为等值点.例如点
(1,1),(-2,-2),(![]() ,
,![]() ),…,都是等值点.已知二次函数
),…,都是等值点.已知二次函数![]() 的
的
图象上有且只有一个等值点![]() ,且当m≤x≤3时,函数
,且当m≤x≤3时,函数 ![]() 的最小值为-9,最大值为-1,则m的取值范围是__________.
的最小值为-9,最大值为-1,则m的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现与证明)![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,连结
,连结![]() .
.
结论1:![]() 与
与![]() 重叠部分的图形是等腰三角形;
重叠部分的图形是等腰三角形;
结论2:![]() .
.
试证明以上结论.
(应用与探究)
在![]() 中,已知
中,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,连结
,连结![]() .若以
.若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求
为顶点的四边形是正方形,求![]() 的长.(要求画出图形)
的长.(要求画出图形)

查看答案和解析>>
科目:初中数学 来源: 题型:
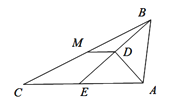
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱中,标有4,5,6的三个球放入乙箱中.
(1)小宇从甲箱中随机模出一个球,求“摸出标有数字是3的球”的概率;
(2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字大1,则称小宇“略胜一筹”.请你用列表法(或画树状图)求小宇“略胜一筹”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com