Question

【题目】在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为等值点．例如点

（1，1），(－2，－2)，(，)，…，都是等值点．已知二次函数的

图象上有且只有一个等值点 ，且当m≤x≤3时，函数 的最小值为－9，最大值为－1，则m的取值范围是__________．

Answer 1

【答案】

【解析】根据等值点的概念令ax2+4x+c=x，即ax2+3x+c=0，由题意，△=32-4ac=0，即4ac=9，方程的根为=，从而求得a=-2，c=-，所以函数y=ax2+4x+c-=-2x2+4x-3，根据函数解析式求得顶点坐标，根据y的取值，即可确定x的取值范围．

令ax2+4x+c=x，即ax2+3x+c=0，
由题意，△=32-4ac=0，即4ac=9，
又方程的根为=，
解得a=-2，c=-．
故函数y=ax2+4x+c-=-2x2+4x-3=-2（x-1）2-1，
如图，该函数图象顶点为（1，-1），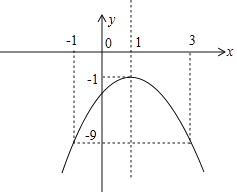

由于函数图象在对称轴x=1左侧y随x的增大而增大，在对称轴右侧y随x的增大而减小，
且当m≤x≤3时，函数y=-2x2+4x-3的最小值为-9，最大值为-1，
∴-1≤m≤1，
故答案为：-1≤m≤1．