
【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?

【答案】(1)BD=MF,BD⊥MF.理由见解析;
(2)β的度数为60°或15°;
(3)平移的距离是(6﹣2![]() )cm.
)cm.
【解析】
试题(1)有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),得BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.
(2)根据旋转的性质得出结论.
(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出:![]() ,解得A2A的大小.
,解得A2A的大小.
试题解析:(1)BD=MF,BD⊥MF.
延长FM交BD于点N,
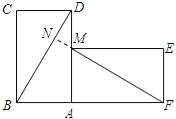
由题意得:△BAD≌△MAF.
∴BD=MF,∠ADB=∠AFM.
又∵∠DMN=∠AMF,
∴∠ADB+∠DMN=∠AFM+∠AMF=90°,
∴∠DNM=90°,
∴BD⊥MF;
(2)当AK=FK时,∠KAF=∠F=30°,
则∠BAB1=180°﹣∠B1AD1﹣∠KAF=180°﹣90°﹣30°=60°,
即β=60°;
②当AF=FK时,∠FAK=![]() =75°,
=75°,
∴∠BAB1=90°﹣∠FAK=15°,
即β=15°;
∴β的度数为60°或15°;
(3)由题意得矩形PNA2A.设A2A=x,则PN=x,
在Rt△A2M2F2中,∵F2M2=FM=8,
∴A2M2=4,A2F2=4![]() ,∴AF2=4
,∴AF2=4![]() ﹣x.
﹣x.
∵∠PAF2=90°,∠PF2A=30°,
∴AP=AF2tan30°=4﹣![]() x.
x.
∴PD=AD﹣AP=4![]() ﹣4+
﹣4+![]() x.
x.
∵NP∥AB,
∴∠DNP=∠B.
∵∠D=∠D,
∴△DPN∽△DAB.
∴![]() .
.
∴![]() ,
,
解得x=6﹣2![]() .
.
即A2A=6﹣2![]() .
.
答:平移的距离是(6﹣2![]() )cm.
)cm.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为等值点.例如点
(1,1),(-2,-2),(![]() ,
,![]() ),…,都是等值点.已知二次函数
),…,都是等值点.已知二次函数![]() 的
的
图象上有且只有一个等值点![]() ,且当m≤x≤3时,函数
,且当m≤x≤3时,函数 ![]() 的最小值为-9,最大值为-1,则m的取值范围是__________.
的最小值为-9,最大值为-1,则m的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
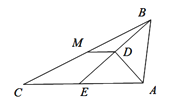
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
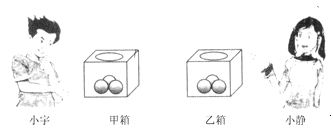
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱中,标有4,5,6的三个球放入乙箱中.
(1)小宇从甲箱中随机模出一个球,求“摸出标有数字是3的球”的概率;
(2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字大1,则称小宇“略胜一筹”.请你用列表法(或画树状图)求小宇“略胜一筹”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com