练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

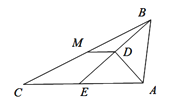
    【题目】如图，在△ABC中，点E是边AC上一点，线段BE垂直于∠BAC的平分线于点D，点M为边BC的中点，连接DM．

    (1)求证: DM＝CE；

    (2)若AD＝6，BD＝8，DM＝2，求AC的长．

    【答案】（1）见解析 （2）AC=14

    【解析】

    （1）证△BAD≌△EAD，推出AB=AE，BD=DE，根据三角形的中位线性质得出DM=CE即可；
    （2）根据勾股定理求出AB，求出AE，根据三角形的中位线求出CE，即可得出答案．

    ∵AD⊥BE，
    ∴∠ADB=∠ADE=90°，
    ∵AD为∠BAC的平分线，
    ∴∠BAD=∠EAD，
    在△BAD和△EAD中，

    ，
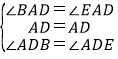    ∴△BAD≌△EAD（SAS），
    ∴AB=AE，BD=DE，
    ∵M为BC的中点，
    ∴DM=CE
    （2）∵在Rt△ADB中，∠ADB=90°，AD=6，BD=8，
    ∴由勾股定理得：AE=AB=，
    ∵DM=2，DM=CE，
    ∴CE=4，
    ∴AC=10+4=14．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用“”规定一种新运算：对于任意有理数a和b，规定ab＝ab+2ab+a． 如：13＝1×3+2×1×3+1＝16

    （1）求3（﹣1）的值；

    （2）若（a+1）2＝36，求a的值；

    （3）若m＝2x，n＝（x）3（其中x为有理数），试比较m、n的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

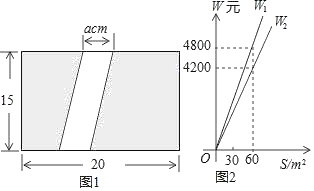
    【题目】如图1，为美化校园环境，某校计划在一块长为20m，宽为15m的长方形空地上修建一条宽为a（m）的甬道，余下的部分铺设草坪建成绿地．

    （1）甬道的面积为　 　m2，绿地的面积为　 　m2（用含a的代数式表示）；

    （2）已知某公园公司修建甬道，绿地的造价W1（元），W2（元）与修建面积S之间的函数关系如图2所示．①园林公司修建一平方米的甬道，绿地的造价分别为　 　元，　 　元．②直接写出修建甬道的造价W1（元），修建绿地的造价W2（元）与a（m）的关系式；③如果学校决定由该公司承建此项目，并要求修建的甬道宽度不少于2m且不超过5m，那么甬道宽为多少时，修建的甬道和绿地的总造价最低，最低总造价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嘉嘉将长为20cm，宽为10cm的长方形白纸，按图所示方法粘合起来，粘合部分（图上阴影部分）的宽为3cm．

    （1）求5张白纸粘合后的长度；

    （2）设x张白纸粘合后总长为ycm．写出y与x之间的函数关系式；

    （3）求当x=20时的y值，并说明它在题目中的实际意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】课本拓展

    旧知新意：

    我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？

    1．尝试探究：

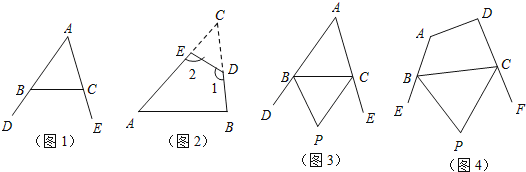
    （1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？

    2．初步应用：

    （2）如图2，在△ABC纸片中剪去△CED，得到四边形ABDE，∠1=130°，则∠2-∠C= ；

    （3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案 ．

    3拓展提升：

    （4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可直接使用，不需说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：A＝2a2＋3ab－2a－1，B＝－a2＋ab＋1.

    (1)若 |a+1| b- 22 0 ，求4A－(3A－2B)的值；

    (2)若(1)中代数式的值与a的取值无关，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤，下面是爸爸妈妈的对话：

    妈妈：“上个月萝卜的单价是元/斤，排骨的单价比萝卜的7倍还多2元”；

    爸爸：“今天，报纸上说与上个月相比，萝卜的单价上涨了25%，排骨的单价上涨了20%”

    请根据上面的对话信息回答下列问题：

    （1）请用含的式子填空：上个月排骨的单价是_________元/斤，这个月萝卜的单价是__________元/斤，排骨的单价是______________元/斤。

    （2）列式表示今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元？（结果要求化成最简）

    （3）当＝4，求今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

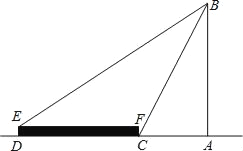
    【题目】如图，在一个平台远处有一座古塔，小明在平台底部的点C处测得古塔顶部B的仰角为60°，在平台上的点E处测得古塔顶部的仰角为30°．已知平台的纵截面为矩形DCFE，DE=2米，DC=20米，求古塔AB的高（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，解答下列问题：

    例：当a=5，则|a|=|5|=5，故此时a的绝对值是它本身；当a=0时，|a|=0，故此时a的绝对值是0；当a＜0时，如a=﹣5，则|a|=|－5|=﹣（－5）=5，故此时a的绝对值是它的相反数．请仿照图例中的分类讨论，解决下面的问题：

    （1）|﹣4+5|=　 　；|﹣﹣3|=　 　；

    （2）如果|x+1|=2，求x的值；

    （3）若数轴上表示数a的点位于﹣3与5之间，求|a+3|+|a﹣5|的值.

    查看答案和解析>>

    同步练习册答案