
����Ŀ���α���չ
��֪���⣺
��������֤���������ε�һ����ǵ������������ڵ������ڽǵĺͣ���ô�������ε�һ���ڽ����������ڵ�������ǵĺ�֮�����������������ϵ�أ�
1������̽����
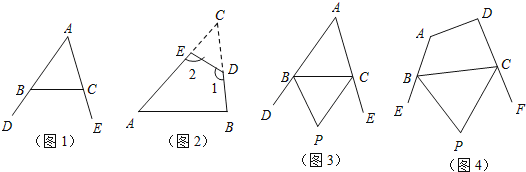
��1����ͼ1����DBC����ECB�ֱ�Ϊ��ABC��������ǣ���̽����A����DBC+��ECB֮�����������������ϵ��Ϊʲô��
2������Ӧ�ã�
��2����ͼ2������ABCֽƬ�м�ȥ��CED���õ��ı���ABDE����1=130��������2-��C= ��
��3��С�����뵽�����������һ�����⣺��ͼ3������ABC�У�BP��CP�ֱ�ƽ�������DBC����ECB����P����A�к�������ϵ������������Ľ���ֱ��д���� ��
3��չ������
��4����ͼ4�����ı���ABCD�У�BP��CP�ֱ�ƽ�������EBC����FCB����P����A����D�к�������ϵ��Ϊʲô��������Ҫ��������Ľ���˵������ֱ��ʹ�ã�����˵��������
���𰸡���1����DBC+��ECB=180��+��A����2��50������3����P=90��-![]() ��A����4����BAD+��CDA=360��-2��P��
��A����4����BAD+��CDA=360��-2��P��
��������
�����������1�����������ε�һ����ǵ������������ڵ������ڽǵĺͱ�ʾ����DBC+��ECB���������������ڽǺͶ����������ɵý⣻
��2��������1���Ľ����������㼴�ɵý⣻
��3����ʾ����DBC+��ECB���ٸ��ݽ�ƽ���ߵĶ��������PBC+��PCB��Ȼ�������������ڽǺͶ�����ʽ�������ɵý⣻
��4���ӳ�BA��CD�ཻ�ڵ�Q��������Q��ʾ����P��������1���Ľ����������ɵý⣮
�����������1����DBC+��ECB
=180��-��ABC+180��-��ACB
=360��-����ABC+��ACB��
=360��-��180��-��A��
=180��+��A��
��2���ߡ�1+��2=��180��+��C��
��130��+��2=180��+��C��
���2-��C=50����
��3����DBC+��ECB=180��+��A��
��BP��CP�ֱ�ƽ�������DBC����ECB��
���PBC+��PCB=![]() ����DBC+��ECB��=
����DBC+��ECB��=![]() ��180��+��A����
��180��+��A����
����PBC����P=180��-![]() ��180��+��A��=90��-
��180��+��A��=90��-![]() ��A��
��A��
����P=90��-![]() ��A��
��A��
��4���ӳ�BA��CD��Q��
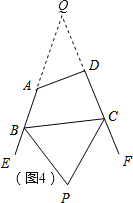
����P=90��-![]() ��Q��
��Q��
���Q=180��-2��P��
���BAD+��CDA=180��+��Q��
=180��+180��-2��P��
=360��-2��P��


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�ϵʽ�У����ú�x�Ĵ���ʽ��ʾy���ǣ�������
A.y=2x��3y
B.x=2��3y
C.��y=2x��1
D.y=x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x�ύ��A����3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��

��1������κ����Ľ���ʽ��
��2������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
��3����ֱ����y��Ľ���ΪE������AD��AE������ADE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̫���뾶ԼΪ696 000 km����696 000�ÿ�ѧ��������ʾΪ( )
A. 6.96��105 B. 69.6��104 C. 6.96��103 D. 0.696��108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ2��3xy+4xy2�Ĵ�������ߴ����ϵ���ֱ��ǣ�������
A.2����3
B.��3��4
C.3��4
D.3����3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com