
【题目】阅读材料,解答下列问题:
例:当a=5,则|a|=|5|=5,故此时a的绝对值是它本身;当a=0时,|a|=0,故此时a的绝对值是0;当a<0时,如a=﹣5,则|a|=|-5|=﹣(-5)=5,故此时a的绝对值是它的相反数.请仿照图例中的分类讨论,解决下面的问题:
(1)|﹣4+5|= ;|﹣![]() ﹣3|= ;
﹣3|= ;
(2)如果|x+1|=2,求x的值;
(3)若数轴上表示数a的点位于﹣3与5之间,求|a+3|+|a﹣5|的值.
科目:初中数学 来源: 题型:
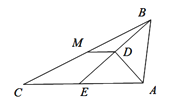
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料1:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号.如:![]()
![]() ;
;
材料2: 配方法是初中数学思想方法中的一种重要的解题方法。配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题。它的应用非常广泛,在解方程、求最值、证明等式、化简根式、因式分解等方面都经常用到。
如:![]()
∵![]() ,∴
,∴![]() 即
即![]()
∴![]() 的最小值为1.
的最小值为1.
根据以上材料解决下列问题:
(1)填空:![]() =________________;
=________________;![]() =______________;
=______________;
(2)求![]() 的最小值;
的最小值;
(3)已知![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则![]() ;③ 若
;③ 若![]() ,则
,则![]() 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则![]() 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

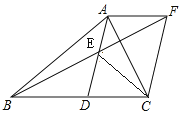
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线:![]() 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
(1)求双曲线与抛物线的解析式;
(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
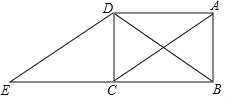
【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
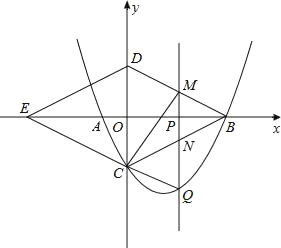
如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com