Question

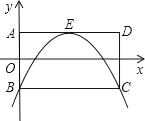
【题目】在矩形ABCD中，AB=2，AD=4，以AB的垂直平分线为x轴，AB所在的直线为y轴，建立如图所示的平面直角坐标系．

（1）求点的坐标：A　 　，B　 　，C　 　，　 　，AD的中点E　 　；

（2）求以E为顶点，对称轴平行于y轴，并且经过点B，C的抛物线的解析式；

（3）求对角线BD与上述抛物线除点B以外的另一交点P的坐标；

（4）△PEB的面积S△PEB与△PBC的面积S△PBC具有怎样的关系？证明你的结论．

Answer 1

【答案】(1) A（0，1），B（0，﹣1），C（4，﹣1），D（4，1），E（2，1）；(2) 抛物线y=﹣（x﹣2）2+1经过点C（4，﹣1）；(3) P（3，）；(4) S△PEB=S△PBC,理由见解析

【解析】

（1）根据题意和图象可知OA=OB=1，AD=BC=4，所以（0，1），B（0，-1），C（4，-1），D（4，1），E（2，1）；
（2）根据题意可设抛物线的解析式为y=a（x-2）2+1，把点B（0，-1）代入可得a=-，即可求得二次函数的解析式；
（3）利用直线BD的解析式为y=x-1，和抛物线解析式联立成方程组即可求得交点P的坐标；

（4）分别求出S△PEB和S△PEB，从而得出S△PEB=S△PBC;

解：（1）A（0，1），B（0，﹣1），C（4，﹣1），D（4，1），E（2，1）；

（2）设抛物线的解析式为y=a（x﹣2）2+1，

∵抛物线经过点B（0，﹣1），

∴a（0﹣2）2+1=﹣1，解得a=﹣，

∴抛物线的解析式为y=﹣（x﹣2）2+1，

经验证，抛物线y=﹣（x﹣2）2+1经过点C（4，﹣1）；

（3）直线BD的解析式为y=x﹣1，解方程组得点P的坐标：P（3，）；

（4）S△PEB=S△PBCS△PBC=×4×=3，S△PEB=×（1×2+1×1）=，

∴S△PEB=S△PBC．