
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
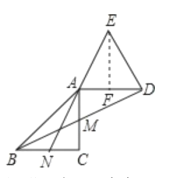
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;
(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC即可得证;
②过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,得∠NAC=∠AEF,由(1)可知
,得∠NAC=∠AEF,由(1)可知![]() ,
,![]() 则可证
则可证![]() ,可证
,可证![]() ≌
≌![]() ,据此知
,据此知![]() ,再证
,再证![]() ,又
,又![]() 得
得![]() ,又因为
,又因为![]() ,从而得
,从而得![]() ,即可得证.
,即可得证.
(1)∵![]() 是
是![]() 中点
中点
∴![]()
又∵![]()
![]()
∴在![]() 与
与![]() 中
中
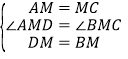
∴![]() ≌
≌![]() (
(![]() )
)
(2)① ![]()
![]() 是等腰直角三角形
是等腰直角三角形
∴ ![]()
∵ ![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点
中点
∴ ![]() ,
,![]()
∴ ![]()
又∵![]()
∴在![]() 与
与![]() 中
中
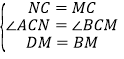
∴![]() ≌
≌![]() (
(![]() )
)
② 过点![]() 作
作![]() 交
交![]() 于点
于点![]()
∵ ![]()
∴ ![]()
由(1)可知![]() ≌
≌![]()
∴ ![]() ,
,![]()
∴ ![]()
∴ ![]()
在![]() 和
和![]() 中
中
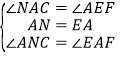
∴ ![]() ≌
≌![]() (
(![]() )
)
∴ ![]() ,
,![]() ,
,![]()
∵ ![]() 为
为![]() 中点
中点
∴ ![]() 为
为![]() 中点
中点
∴ ![]() 垂直平分
垂直平分![]()
∴ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
即![]()
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.

小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
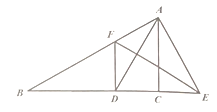
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 平分线,
平分线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 延长线于点
延长线于点![]() .求证:
.求证:![]() .
.
证明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分线的定义)
(角平分线的定义)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)
∴![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(t,0)是x轴上的动点,Q(0,2t)是y轴上的动点.若线段PQ与函数y=﹣|x|2+2|x|+3的图象只有一个公共点,则t的取值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
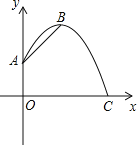
【题目】一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
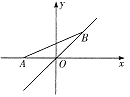
【题目】如图,点A的坐标为(-1,0),点B在直线![]() 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
A. (0,0) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com