
����Ŀ����ͼ��������ABCD�У�AB=4cm����BAD=60�㣮����E��F�ֱ�ӵ�B��Dͬʱ��������1cm/s���ٶ����A��C�˶�������AF��CE��ȡAF��CE���е�G��H������GE��FH�����˶���ʱ��Ϊts��0��t��4����
��1����֤��AF��CE��
��2����tΪ��ֵʱ���ı���EHFGΪ���Σ�
��3����̽�����Ƿ����ij��ʱ��t��ʹ�ı���EHFGΪ���Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��֤������������2��t=1����3��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�
��������
��1���������ε����ʵõ���B=��D��AD=BC��AB��DC���Ƴ���ADF�ա�CBE������ȫ�������ε����ʵõ���DFA=��BEC������ƽ���ߵ��ж��������ɵõ����ۣ�
��2����D��DM��AB��M������GH��EF���Ƴ��ı���AECF��ƽ���ı��Σ��������ε��ж��������ɵõ��ı���EGFH�����Σ�֤���ı���DMEF�Ǿ��Σ����ǵõ�ME=DF=t�з��̼��ɵõ����ۣ�
��3�������ڣ��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ����ݾ��ε������з��̼��ɵõ������
��1��֤�����߶���E��Fͬʱ�˶����ٶ���ȣ�
��DF=BE��
���ı���ABCD�����Σ�
���B=��D��AD=BC��AB��DC��
����ADF����CBE��
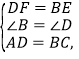
���ADF�ա�CBE��
���DFA=��BEC��
��AB��DC��
���DFA=��FAB��
���FAB=��BEC��
��AF��CE��
��2����D��DM��AB��M������GH��EF��
��DF=BE=t��
��AF��CE��AB��CD��
���ı���AECF��ƽ���ı��Σ�
��G��H��AF��CE���е㣬
��GH��AB��
���ı���EGFH�����Σ�
��GH��EF��
��EF��AB����FEM=90�㣬
��DM��AB��
��DM��EF��
���ı���DMEF�Ǿ��Σ�
��ME=DF=t��
��AD=4����DAB=60�㣬DM��AB��
��![]()
��BE=4��2��t=t��
��t=1��
��3�������ڣ��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�
���ı���EHFGΪ���Σ�
��EF=GH��
��EF2=GH2��
��![]() ���t=0��0��t��4��
���t=0��0��t��4��
����ԭ����ì�ܣ�
�����ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�


 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
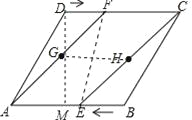
����Ŀ����֪������ABCD�У�AB��4��BC��3����M��N�ֱ��ڱ�AB��CD�ϣ�ֱ��MN�����ζԽ��� AC�ڵ�E������AME��ֱ��MN���ۣ���A���ڵ�P�����ҵ�P������CB��.
(1)��ͼ1����EP��BCʱ����CN�ij���
(2) ��ͼ2����EP��ACʱ����AM�ij���
(3) ��д���߶�CP�ij���ȡֵ��Χ������CP�ij����ʱMN�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
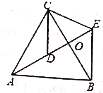
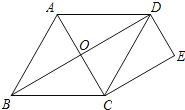
����Ŀ����ͼ����ACB�͡�DCE��Ϊ���������Σ���A��D��E��ͬһ��ֱ���ϣ�BC��AE�ཻ�ڵ�O������BE������CAB=��CBA=��CDE=��CED=50�㡣
��1����֤��AD=BE��
��2�����AEB������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪����x,y�ķ�����![]() �Ľ�������
�Ľ�������
��1����a��ȡֵ��Χ
��2������|4a+5|-|a-4|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ��߽��ڵ�O����E��������һ�㣬DE��AC��CE��BD��
��1����֤���ı���DECO�Ǿ��Σ�
��2������AE��BD�ڵ�F������ADB��30�㣬DE��2ʱ����AF�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2017������)�������������������(�� ��)
A. ��һ��������1��2��3��4��5�������ķ�����3
B. ����ʽ����![]() ��������������������1
��������������������1
C. �Խ����ഹֱ���ı�����˳�����������ı��е������ı���������
D. ��һ���ǵ����߷ֱ�����һ���ǵ�����ƽ�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A������ B��ƹ����C����ë�� D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ��

��ش��������⣺
��1����α������ѧ�����ж����ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �У������ڽǵ�ƽ���߽��ڵ�
�У������ڽǵ�ƽ���߽��ڵ�![]() .����
.����![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() .
.

��1����ͼ1��
����![]() ����
����![]() ___________��
___________��![]() _____________��
_____________��
�ڲ���![]() ��
��![]() �Ĺ�ϵ����˵��������ɣ�
�Ĺ�ϵ����˵��������ɣ�
��2����ͼ2����![]() ���
���![]() ��ƽ���߽�
��ƽ���߽�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() .��
.��![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() ��
��![]() ���е㣬�ӳ�
���е㣬�ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ������
������![]() ����ͼ����.
����ͼ����.

��1����֤��![]() ��
��![]() ��
��
��2����֪��![]() ��
��![]() ���е㣬����
���е㣬����![]() ����ͼ����.
����ͼ����.
����֤:![]() ��
��![]() ��
��
����ͼ�ۣ��ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ������
������![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com