
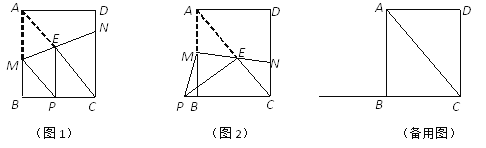
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.
科目:初中数学 来源: 题型:
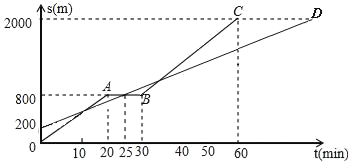
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方形分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
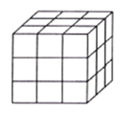
(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。


(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】歼-20(英文:Chengdu J-20,绰号:威龙,北约命名:Fire Fang)是我国自主研发的一款单座、双发动机并具备高隐身性、高态势感知、高机动性等能力的第五代战斗机。


歼-20在机腹部位有一个主弹仓,机身两侧的起落架前方各有一个侧弹仓。歼-20的侧弹舱门为一片式结构,这个弹舱舱门向上开启,弹舱内滑轨的前端向外探出,使导弹头部伸出舱外,再直接点火发射。
如图是歼-20侧弹舱内部结构图,它的舱体横截面是等腰梯形ABCD,AD//BC,AB = CD,BE⊥AD,CF⊥AD,侧弹舱宽AE = 2.3米,舱底宽BC = 3.94米,舱顶与侧弹舱门的夹角∠A = 53.
求(1)侧弹舱门AB的长;
(2)舱顶AD与对角线BD的夹角的正切值.(结果精确到0.01,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级有350名师生需要租车去野外进行拓展训练,现有A、B两种类型号的车可供选择,已知1辆A型车和2辆B型车可载110人,2辆A型车和1辆B型车可载100人。
(1)A、B型车每辆可分别载多少人?
(2)要始每辆车都恰好坐满且正好运完这些师生,请问你有哪几种设计租车方案,请一一列举出来。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数![]() ,
,![]() 定义两种新运算“※”和“
定义两种新运算“※”和“![]() ”:
”: ![]() ※
※![]() ,
,![]() (其中
(其中![]() 为常数,且
为常数,且![]() ,若对于平面直角坐标系
,若对于平面直角坐标系![]() 中的点
中的点![]() ,有点
,有点![]() 的坐标
的坐标![]() ※
※![]() ,
,![]() 与之对应,则称点
与之对应,则称点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() .例如:
.例如:![]() 的“2衍生点”为
的“2衍生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“3衍生点”的坐标为 ;
的“3衍生点”的坐标为 ;
(2)若点![]() 的“5衍生点”
的“5衍生点” ![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() ,且直线
,且直线![]() 平行于
平行于![]() 轴,线段
轴,线段![]() 的长度为线段
的长度为线段![]() 长度的3倍,求
长度的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com