
ΓΨΧβΡΩΓΩΘ®7Ζ÷Θ©Ρ≥÷–―ß1000Οϊ―ß…ζ≤ΈΦ”ΝΥΓ±ΜΖ±Θ÷Σ ΕΨΚ»ϋΓΑΘ§ΈΣΝΥΝΥΫβ±Ψ¥ΈΨΚ»ϋ≥…Φ®«ιΩωΘ§¥”÷–≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΒΡ≥…Φ®Θ®ΒΟΖ÷»Γ’ϊ ΐΘ§¬ζΖ÷ΈΣ100Ζ÷Θ©ΉςΈΣ―υ±ΨΫχ––Ά≥ΦΤΘ§≤Δ÷ΤΉςΝΥ»γΆΦΤΒ ΐΖ÷≤Φ±μΚΆΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ®≤ΜΆξ’ϊ«“Ψ÷≤ΩΈέΥπΘ§Τδ÷–ΓΑΓωΓ±±μ Ψ±ΜΈέΥπΒΡ ΐΨίΘ©Θ°«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
≥…Φ®Ζ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
50ΓήxΘΦ60 | 8 | 0.16 |
60ΓήxΘΦ70 | 12 | a |
70ΓήxΘΦ80 | Γω | 0.5 |
80ΓήxΘΦ90 | 3 | 0.06 |
90ΓήxΓή100 | b | c |
ΚœΦΤ | Γω | 1 |
Θ®1Θ©–¥≥ωaΘ§bΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©«κΙάΦΤ’β1000Οϊ―ß…ζ÷–”–Εύ…Ό»ΥΒΡΨΚ»ϋ≥…Φ®≤ΜΒΆ”Ύ70Ζ÷ΘΜ
Θ®3Θ©‘Ύ―Γ»ΓΒΡ―υ±Ψ÷–Θ§¥”ΨΚ»ϋ≥…Φ® «80Ζ÷“‘…œΘ®Κ§80Ζ÷Θ©ΒΡΆ§―ß÷–ΥφΜζ≥ι»ΓΝΫΟϊΆ§―ß≤ΈΦ”ΜΖ±Θ÷Σ Ε–ϊ¥ΪΜνΕ·Θ§«σΥυ≥ι»ΓΒΡ2ΟϊΆ§―ßά¥Ή‘Ά§“ΜΉιΒΡΗ≈¬ Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©a=0.24Θ§b=2Θ§c=0.04ΘΜΘ®2Θ©600»ΥΘΜΘ®3Θ©![]() »Υ.
»Υ.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο50ΓήxΘΦ60ΒΡΤΒ ΐΚΆΤΒ¬ Θ§ΗυΨίΙΪ ΫΘΚΤΒ¬ ΘΫΤΒ ΐΓ¬Ήή ΐœ»ΦΤΥψ≥ω―υ±ΨΉή»Υ ΐΘ§‘ΌΖ÷±πΦΤΥψ≥ωaΘ§bΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©œ»ΦΤΥψ≥ωΨΚ»ϋΖ÷ ΐ≤ΜΒΆ”Ύ70Ζ÷ΒΡΤΒ¬ Θ§ΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΥΦœκΘ§ΦΤΥψ≥ω1000Οϊ―ß…ζ÷–ΨΚ»ϋ≥…Φ®≤ΜΒΆ”Ύ70Ζ÷ΒΡ»Υ ΐΘΜ
Θ®3Θ©Ν– ς–ΈΆΦΜρΝ–≥ω±μΗώΘ§ΒΟΒΫ“Σ«σΒΡΥυ”–«ιΩωΚΆ2ΟϊΆ§―ßά¥Ή‘“ΜΉιΒΡ«ιΩωΘ§άϊ”Ο«σΗ≈¬ ΙΪ ΫΦΤΥψ≥ωΗ≈¬ .
Θ®1Θ©―υ±Ψ»Υ ΐΈΣΘΚ8Γ¬0.16=50Θ®ΟϊΘ©
a=12Γ¬50=0.24Θ§
70ΓήxΘΦ80ΒΡ»Υ ΐΈΣΘΚ50ΓΝ0.5=25Θ®ΟϊΘ©
b=50©¹8©¹12©¹25©¹3=2Θ®ΟϊΘ©
c=2Γ¬50=0.04
Υυ“‘a=0.24Θ§b=2Θ§c=0.04ΘΜ
Θ®2Θ©‘Ύ―Γ»ΓΒΡ―υ±Ψ÷–Θ§ΨΚ»ϋΖ÷ ΐ≤ΜΒΆ”Ύ70Ζ÷ΒΡΤΒ¬ «0.5+0.06+0.04=0.6Θ§ΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΥΦœκΘ§”–ΘΚ
1000ΓΝ0.6=600Θ®»ΥΘ©
Γύ’β1000Οϊ―ß…ζ÷–”–600»ΥΒΡΨΚ»ϋ≥…Φ®≤ΜΒΆ”Ύ70Ζ÷ΘΜ
Θ®3Θ©≥…Φ® «80Ζ÷“‘…œΒΡΆ§―ßΙ≤”–5»ΥΘ§Τδ÷–ΒΎ4Ήι”–3»ΥΘ§≤ΜΖΝΦ«ΈΣΦΉΘ§““Θ§±ϊΘ§ΒΎ5Ήι”–2»ΥΘ§≤ΜΖΝΦ«ΉςAΘ§B
¥”ΨΚ»ϋ≥…Φ® «80Ζ÷“‘…œΘ®Κ§80Ζ÷Θ©ΒΡΆ§―ß÷–ΥφΜζ≥ι»ΓΝΫΟϊΆ§―ßΘ§«ι–Έ»γ ς–ΈΆΦΥυ ΨΘ§Ι≤”–20÷÷«ιΩωΘΚ
≥ι»ΓΝΫΟϊΆ§―ß‘ΎΆ§“ΜΉιΒΡ”–ΘΚΦΉ““Θ§ΦΉ±ϊΘ§““ΦΉΘ§““±ϊΘ§±ϊΦΉΘ§±ϊ““Θ§ABΘ§BAΙ≤8÷÷«ιΩωΘ§
Γύ≥ι»ΓΒΡ2ΟϊΆ§―ßά¥Ή‘Ά§“ΜΉιΒΡΗ≈¬ P=![]() =
=![]()



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ»―ϋ÷±Ϋ«ΓςABCΘ§ΓςMAD÷–Θ§ΓœBAC=ΓœDMA=90ΓψΘ§Ν§Ϋ”BMΘ§CDΘ°«“BΘ§MΘ§D»ΐΒψΙ≤œΏ

Θ®1Θ©Β±ΒψDΘ§ΒψM‘ΎBC±Ώœ¬ΖΫΘ§CDΘΦBD ±Θ§»γΆΦΔΌΘ§«σ÷ΛΘΚBM+CD=AMΘΜΘ®Χα ΨΘΚ―”≥ΛDBΒΫΒψNΘ§ ΙMN=MDΘ§Ν§Ϋ”ANΘ°Θ©
Θ®2Θ©Β±ΒψD‘ΎAC±Ώ”“≤ύΘ§ΒψM‘ΎΓςABCΡΎ≤Ω ±Θ§»γΆΦΔΎΘΜΒ±ΒψD‘ΎAB±ΏΉσ≤ύΘ§ΒψM‘ΎΓςABCΆβ≤Ω ±Θ§»γΆΦΔέΘ§«κ÷±Ϋ”–¥≥ωœΏΕΈBMΘ§CDΘ§AM÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Μ–η“Σ÷ΛΟςΘΜ
Θ®3Θ©‘ΎΘ®1Θ©Θ§Θ®2Θ©ΧθΦΰœ¬Θ§ΒψE «AB÷–ΒψΘ§MF «ΓςAMDΒΡΫ«ΤΫΖ÷œΏΘ§Ν§Ϋ”EFΘ§»τEF=2MF=6Θ§‘ρCD=ΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ΓœABC=90ΓψΘ§AC=25cmΘ§BC=15cm
(1)…ηΒψP‘ΎAB…œ,»τΓœPAC =ΓœPCA.«σAPΒΡ≥ΛΘΜ
(2)…ηΒψM‘ΎAC…œ.»τΓςMBCΈΣΒ»―ϋ»ΐΫ«–ΈΘ§«σAMΒΡ≥Λ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
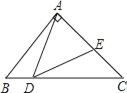
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ΓœBAC=90ΓψΘ§AB=AC=1Θ§ΒψD «BC…œ“ΜΗωΕ·ΒψΘ®≤Μ”κBΓΔC÷ΊΚœΘ©Θ§‘ΎAC…œ»ΓEΒψΘ§ ΙΓœADE=45ΓψΘ°
Θ®1Θ© ‘≈–ΕœΓςABD”κΓςDCE «ΖώœύΥΤ≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©…ηBD=xΘ§AE=yΘ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘΜ≤Δ÷Η≥ωΒ±ΒψD‘ΎBC…œ‘ΥΕ·Θ®≤Μ”κBΓΔC÷ΊΚœΘ© ±Θ§AE «Ζώ¥φ‘ΎΉν–Γ÷ΒΘΩ»τ¥φ‘ΎΘ§«σ≥ωΉν–Γ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…ΘΜ
Θ®3Θ©Β±ΓςADE «Β»―ϋ»ΐΫ«–Έ ±Θ§«σAEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏy=ax2+bxΙΐΒψAΘ®1Θ§4Θ©ΓΔBΘ®©¹3Θ§0Θ©Θ§ΙΐΒψAΉς÷±œΏACΓΈx÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΝμ“ΜΒψCΘ§‘Ύx÷α…œ”–“ΜΒψDΘ®4Θ§0Θ©Θ§Ν§Ϋ”CDΘ°

Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»τ‘Ύ≈ΉΈοœΏ…œ¥φ‘ΎΒψQΘ§ ΙΒΟCDΤΫΖ÷ΓœACQΘ§«κ«σ≥ωΒψQΒΡΉχ±ξΘΜ
Θ®3Θ©‘Ύ÷±œΏCDΒΡœ¬ΖΫΒΡ≈ΉΈοœΏ…œ»Γ“ΜΒψNΘ§ΙΐΒψNΉςNGΓΈy÷αΫΜCD”ΎΒψGΘ§“‘NGΈΣ÷±ΨΕΜ≠‘≤‘Ύ÷±œΏCD…œΫΊΒΟœ“GHΘ§Έ œ“GHΒΡΉν¥σ÷Β «Εύ…ΌΘΩ
Θ®4Θ©“ΜΕ·ΒψP¥”CΒψ≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊC©¹A©¹D‘ΥΕ·Θ§‘ΎœΏΕΈCD…œΜΙ”–“ΜΕ·ΒψMΘ§Έ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ ΙPM+AM=4ΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§»γΆΦΓςABCΚΆΓςCDEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§BΓΔCΓΔD»ΐΒψ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§Ν§Ϋ”œΏΕΈBEΓΔADΫΜ”ΎΒψFΘ§Ν§Ϋ”CFΘ§

Θ®1Θ©«σ÷ΛΘΚΓœFBC=ΓœFAC.
Θ®2Θ©«σΓœBFCΒΡΕ» ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=©¹x2+bx+cΘ®aΓΌ0Θ©”κx÷αΫΜ”ΎΒψAΘ®©¹1Θ§0Θ©ΚΆBΘ®3Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψDΒΡΚαΉχ±ξΈΣmΘ®0ΘΦmΘΦ3Θ©Θ§Ν§ΫαDC≤Δ―”≥Λ÷ΝEΘ§ ΙΒΟCE=CDΘ§Ν§ΫαBEΘ§BCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨΒψEΒΡΉχ±ξΘ§≤Δ«σ≥ωΒψEΉίΉχ±ξΒΡΖΕΈßΘΜ
Θ®3Θ©«σΓςBCEΒΡΟφΜΐΉν¥σ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫBCΘ§÷±œΏMNΨ≠ΙΐΒψCΘ§«“ADΓΆMN”ΎΒψDΘ§BEΓΆMN”ΎΒψEΘ°

Θ®1Θ©Β±÷±œΏMN»ΤΒψC–ΐΉΣΒΫΆΦ1ΒΡΈΜ÷Ο ±Θ§«σ÷ΛΘΚΔΌΓςADCΓ’ΓςCEBΘΜΔΎDEΘΫAD+BEΘΜ
Θ®2Θ©Β±÷±œΏMN»ΤΒψC–ΐΉΣΒΫΆΦ2ΒΡΈΜ÷Ο ±Θ§ ‘Έ DEΓΔADΓΔBEΨΏ”–‘θ―υΒΡΒ»ΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟςΘΜ
Θ®3Θ©Β±÷±œΏMN»ΤΒψC–ΐΉΣΒΫΆΦ3ΒΡΈΜ÷Ο ±Θ§ ‘Έ DEΓΔADΓΔBEΨΏ”–‘θ―υΒΡΒ»ΝΩΙΊœΒΘΩΘ®«κ÷±Ϋ”–¥≥ω’βΗωΒ»ΝΩΙΊœΒΘ§≤Μ–η“Σ÷ΛΟςΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§CΈΣœΏΕΈAE…œ“ΜΒψΘ®≤Μ”κΒψAΓΔE÷ΊΚœΘ©Θ§‘ΎAEΆ§≤ύΖ÷±πΉςΒ»±ΏΓςABCΚΆΒ»±ΏΓςCDEΘ§Ν§Ϋ”AD”κBEΫΜ”ΎΒψOΘ§AD”κBCΫΜ”ΎΒψPΘ§BE”κCDΫΜ”ΎΒψQΘ§Ν§Ϋ”PQΓΔOCΘ§“‘œ¬ΥΡΗωΫα¬έΘΚΔΌΓςBOCΓ’ΓςEDOΘΜΔΎDEΘΫDPΘΜΔέΓœAOCΘΫΓœCOEΘΜΔήOCΓΆPQΘ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©

A.1ΗωB.2ΗωC.3ΗωD.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com