
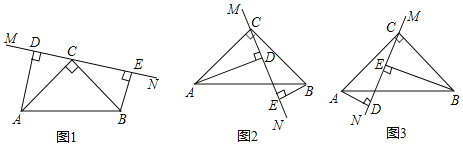
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.

(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系,并加以证明;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?(请直接写出这个等量关系,不需要证明).
【答案】(1)见解析;(2)DE=AD﹣BE,证明见解析;(3)DE=BE﹣AD.
【解析】
(1)由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.
(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,所以DE=CE﹣CD=AD﹣BE.
(3)DE、AD、BE具有的等量关系为:DE=BE﹣AD.证明的方法与(2)相同.
(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
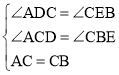 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)DE=AD﹣BE,
在△ADC和△CEB中,
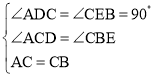 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)结论:DE=BE﹣AD.
同法可得△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CD﹣CE=BE﹣AD.


科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.
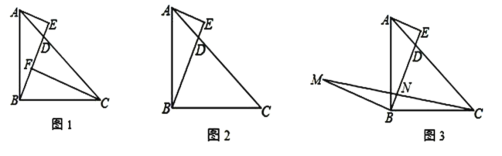
(1) 如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;
(2) 如图 2,若 BC=CD,求证:BD=2AE ;
(3) 如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.

(1)请你写出一个正确的命题,并加以证明;
(2)请你至少写出三个这样的正确命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,……每个正方形四条边上的整点的个数.按此规律推算出正方形A2019B2019C2019D2019四条边上的整点共有_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com