
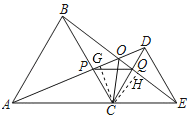
【题目】如图,C为线段AE上一点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,连接AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ、OC,以下四个结论:①△BOC≌△EDO;②DE=DP;③∠AOC=∠COE;④OC⊥PQ.其中正确的结论有( )

A.1个B.2个C.3个D.4个
【答案】A
【解析】
证明△ACD与△BCE全等,可得∠CAD=∠CBE,得出∠AOE=120°,作CG⊥AD于G,CH⊥BE于H,证明△ACG≌△BCH(AAS),得出CG=CH,证出OC平分∠AOE,∠AOC=∠COE,③正确;证出∠BOC≠∠EDO,得出△BOC与△EDO不全等,①错误;证明△ACP≌△BCQ(ASA),得出AP=BQ,PC=QC,可推出DP=EQ,再根据△DEQ的角度关系DE≠DP,可得②错误.证出PQ∥AE,推出OC与AE不垂直,得出OC与PQ不垂直,④错误;即可得出答案.
解:∵△ABC和△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴180°﹣∠ECD=180°﹣∠ACB,
即∠ACD=∠BCE,
在△ACD与△BCE中,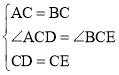 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB=∠ACB=60°,
∴∠AOE=120°,
作CG⊥AD于G,CH⊥BE于H,如图所示:
在△ACG和△BCH中,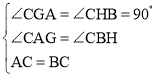 ,
,
∴△ACG≌△BCH(AAS),
∴CG=CH,
∴OC平分∠AOE,
∴∠AOC=∠COE,③正确;
∵∠BOC=∠AOB+∠AOC=120°,∠DOC=∠DOQ+∠COE=120°,
∴∠ODC+∠OCD=60°,
∴∠ODC<60°,
∴∠EDO=∠CDE+∠ODC<120°,
∴∠BOC≠∠EDO,
∴△BOC与△EDO不全等,①错误;
∵∠ACB=∠ECD=60°,
∴∠BCQ=180°﹣60°×2=60°,
∴∠ACB=∠BCQ=60°,
在△ACP与△BCQ中,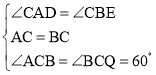 ,
,
∴△ACP≌△BCQ(ASA),
∴AP=BQ,PC=QC,
∵AD=BE,
∴AD﹣AP=BE﹣BQ,
∴DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故②错误.
∵PC=QC,∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ∥AE,
∵∠AOC=60°,
当OC⊥AE时,∠OAC=30°,
则AP平分∠BAC,
而AP不是∠BAC的平分线,
∴OC与AE不垂直,
∴OC与PQ不垂直,④错误;
正确的结论有1个,
故选:A.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,……每个正方形四条边上的整点的个数.按此规律推算出正方形A2019B2019C2019D2019四条边上的整点共有_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,![]() ∥
∥![]() ,坝高10m,迎水坡面
,坝高10m,迎水坡面![]() 的坡度
的坡度![]() ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面![]() 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面![]() 的坡度
的坡度![]() 。
。
 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿
如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于y轴对称的图形△A′B′C′,并写出点A′、B'、C′的坐标;
(2)在图中找一点D,以D、B、C为顶点画三角形,使它与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.(提示:当点D不唯一时,可用D1、D2、D3等加以区别)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为常数,且
为常数,且![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com