
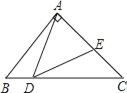
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCЦРЈ¬ЎПBAC=90ЎгЈ¬AB=AC=1Ј¬өгDКЗBCЙПТ»ёц¶ҜөгЈЁІ»УлBЎўCЦШәПЈ©Ј¬ФЪACЙПИЎEөгЈ¬К№ЎПADE=45ЎгЈ®
ЈЁ1Ј©КФЕР¶ПЎчABDУлЎчDCEКЗ·сПаЛЖІўЛөГчАнУЙЈ»
ЈЁ2Ј©ЙиBD=xЈ¬AE=yЈ¬Зуy№ШУЪxөДәҜКэ№ШПөКҪЈ»ІўЦёіцөұөгDФЪBCЙПФЛ¶ҜЈЁІ»УлBЎўCЦШәПЈ©КұЈ¬AEКЗ·сҙжФЪЧоРЎЦөЈҝИфҙжФЪЈ¬ЗуіцЧоРЎЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ»
ЈЁ3Ј©өұЎчADEКЗөИСьИэҪЗРОКұЈ¬ЗуAEөДіӨЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ЎчABDУлЎчDCEПаЛЖЈ¬АнУЙјыЈ»ЈЁ2Ј©x=![]() КұЈ¬yУРЧоРЎЦөЈ¬ЧоРЎЦөОӘ
КұЈ¬yУРЧоРЎЦөЈ¬ЧоРЎЦөОӘ![]() Ј»ЈЁ3Ј©өұЎчADEКЗөИСьИэҪЗРОКұЈ¬AEөДіӨОӘ2©Ғ
Ј»ЈЁ3Ј©өұЎчADEКЗөИСьИэҪЗРОКұЈ¬AEөДіӨОӘ2©Ғ![]() »т
»т![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭөИСьЦұҪЗИэҪЗРОөДРФЦКј°ИэҪЗРОДЪҪЗУлНвҪЗөД№ШПөЈ¬ТЧЦӨЎчABDЎЧЎчDCEЈ®
ЈЁ2Ј©УЙЎчABDЎЧЎчDCEЈ¬¶ФУҰұЯіЙұИАэј°өИСьЦұҪЗИэҪЗРОөДРФЦКҝЙЗуіцyУлxөДәҜКэ№ШПөКҪЈ¬ёщҫЭәҜКэНјПуөД¶ҘөгЧшұкҝЙЗуіцЖдЧоРЎЦөЈ®
ЈЁ3Ј©өұЎчADEКЗөИСьИэҪЗРОКұЈ¬ТтОӘИэҪЗРОөДСьәНөЧІ»ГчИ·Ј¬ЛщТФУҰ·ЦAD=DEЈ¬AE=DEЈ¬AD=AEИэЦЦЗйҝцМЦВЫЈ®
ҪвЈәЈЁ1Ј©ЎчABDУлЎчDCEПаЛЖ
ЎЯЎПBAC=90ЎгЈ¬AB=AC
ЎаЎПB=ЎПC=ЎПADE=45Ўг
ЎЯЎПADC=ЎПB+ЎПBAD=ЎПADE+ЎПCDE
ЎаЎПBAD=ЎПCDE
ЎаЎчABDЎЧЎчDCEЈ»
ЈЁ2Ј©УЙЈЁ1Ј©өГЎчABDЎЧЎчDCE
Ўа![]() Ј¬
Ј¬
ЎЯЎПBAC=90ЎгЈ¬AB=AC=1Ј¬
ЎаBC=![]() Ј¬DC=
Ј¬DC=![]() ©ҒxЈ¬EC=1©Ғy
©ҒxЈ¬EC=1©Ғy
Ўа![]() Ј¬y=x2©Ғ
Ј¬y=x2©Ғ![]() x+1=ЈЁx©Ғ
x+1=ЈЁx©Ғ![]() Ј©2+
Ј©2+![]() Ј¬
Ј¬
өұx=![]() КұЈ¬yУРЧоРЎЦөЈ¬ЧоРЎЦөОӘ
КұЈ¬yУРЧоРЎЦөЈ¬ЧоРЎЦөОӘ![]() Ј»
Ј»
ЈЁ3Ј©өұAD=DEКұЈ¬ЎчABDЎХЎчCDEЈ¬
ЎаBD=CEЈ¬
Ўаx=1©ҒyЈ¬јҙ![]() x©Ғx2=xЈ¬
x©Ғx2=xЈ¬
ЎЯxЎЩ0Ј¬
Ўаx=![]() ©Ғ1
©Ғ1
ЎаAE=1©Ғx=2©Ғ![]() Ј¬
Ј¬
өұAE=DEКұЈ¬DEЎНACЈ¬ҙЛКұDКЗBCЦРөгЈ¬EТІКЗACөДЦРөгЈ¬
ЛщТФЈ¬AE=![]() Ј»
Ј»
өұAD=AEКұЈ¬ЎПDAE=90ЎгЈ¬DУлBЦШәПЈ¬І»әПМвТвЈ»
ЧЫЙПЈ¬өұЎчADEКЗөИСьИэҪЗРОКұЈ¬AEөДіӨОӘ2©Ғ![]() »т
»т![]() Ј®
Ј®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝРЎУұәНРЎәмБҪО»Н¬С§ФЪС§П°Ў°ёЕВКЎұКұЈ¬ЧцН¶ЦАч»ЧУЈЁЦКөШҫщФИөДХэ·ҪМеЈ©КөСйЈ¬ЛыГЗ№ІЧцБЛ![]() ҙОКөСйЈ¬КөСйөДҪб№ыИзПВЈә
ҙОКөСйЈ¬КөСйөДҪб№ыИзПВЈә
іҜЙПөДөгКэ |
|
|
|
|
|
|
іцПЦөДҙОКэ |
|
|
|
|
|
|
![]() јЖЛгЎ°
јЖЛгЎ°![]() өгіҜЙПЎұөДЖөВКәНЎ°
өгіҜЙПЎұөДЖөВКәНЎ°![]() өгіҜЙПЎұөДЖөВКЈ®
өгіҜЙПЎұөДЖөВКЈ®
![]() РЎУұЛөЈәЎ°ёщҫЭКөСйЈ¬Т»ҙОКөСйЦРіцПЦ
РЎУұЛөЈәЎ°ёщҫЭКөСйЈ¬Т»ҙОКөСйЦРіцПЦ![]() өгіҜЙПөДёЕВКЧоҙуЎұЈ»РЎәмЛөЈәЎ°Из№ыН¶ЦА
өгіҜЙПөДёЕВКЧоҙуЎұЈ»РЎәмЛөЈәЎ°Из№ыН¶ЦА![]() ҙОЈ¬ДЗГҙіцПЦ
ҙОЈ¬ДЗГҙіцПЦ![]() өгіҜЙПөДҙОКэХэәГКЗ
өгіҜЙПөДҙОКэХэәГКЗ![]() ҙОЈ®ЎұРЎУұәНРЎәмөДЛө·ЁХэИ·ВрЈҝОӘКІГҙЈҝ
ҙОЈ®ЎұРЎУұәНРЎәмөДЛө·ЁХэИ·ВрЈҝОӘКІГҙЈҝ
![]() РЎУұәНРЎәмёчН¶ЦАТ»Г¶ч»ЧУЈ¬УГБРұн»т»ӯКчЧҙНјөД·Ҫ·ЁЗуіцБҪГ¶ч»ЧУіҜЙПөДөгКэЦ®әНОӘ
РЎУұәНРЎәмёчН¶ЦАТ»Г¶ч»ЧУЈ¬УГБРұн»т»ӯКчЧҙНјөД·Ҫ·ЁЗуіцБҪГ¶ч»ЧУіҜЙПөДөгКэЦ®әНОӘ![]() өДұ¶КэөДёЕВКЈ®
өДұ¶КэөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪөзПЯёЛЙПөДCҙҰТэАӯПЯCEЎўCF№М¶ЁөзПЯёЛЈ¬АӯПЯCEәНөШГжіЙ60ЎгҪЗЈ¬ФЪАлөзПЯёЛ6ГЧөДBҙҰ°ІЦГІвҪЗТЗЈ¬ФЪAҙҰІвөГөзПЯёЛЙПCҙҰөДСцҪЗОӘ30ЎгЈ¬ТСЦӘІвҪЗТЗёЯABОӘ1.5ГЧЈ¬ЗуАӯПЯCEөДіӨЈЁҪб№ыұЈБфёщәЕЈ©Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҫӯ№эФӯөгөДЕЧОпПЯУлxЦбҪ»УЪБнТ»өгЈ¬ёГөгөҪФӯөгөДҫаАлОӘ2Ј¬ЗТёГЕЧОпПЯҫӯ№эЈЁ3Ј¬3Ј©өгЈ¬ФтёГЕЧОпПЯөДҪвОцКҪОӘ____ЎЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЙМөк°ҙҪш»хјЫГҝјю6ФӘ№әҪшТ»Еъ»хЈ¬БгКЫјЫОӘ8ФӘКұЈ¬ҝЙТФВфіц100јюЈ¬Из№ыБгКЫјЫёЯУЪ8ФӘЈ¬ДЗГҙТ»јюТІВфІ»іцИҘЈ¬БгКЫјЫҙУ8ФӘГҝҪөөН0.1ФӘЈ¬ҝЙТФ¶аВфіц10јюЈ®ЙиБгКЫјЫ¶ЁОӘxФӘЈЁ6ЎЬxЎЬ8Ј©Ј®
ЈЁ1Ј©ХвКұұИБгКЫОӘ8ФӘҝЙТФ¶аВфіцјёјюЈҝ
ЈЁ2Ј©ХвКұҝЙТФВфіц¶аЙЩјюЈҝ
ЈЁ3Ј©ХвКұЛщ»сАыИуyЈЁФӘЈ©УлБгКЫјЫxЈЁФӘЈ©өД№ШПөКҪФхСщЈҝ
ЈЁ4Ј©ОӘБгКЫјЫ¶ЁОӘ¶аЙЩКұЈ¬Лщ»сАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ABЎОDEЈ¬ACЎОDFЈ¬AC=DFПВБРМхјюЦРЈ¬І»ДЬЕР¶ПЎчABCЎХЎчDEFөДКЗЈЁЎЎЎЎЈ©

A. AB=DE B. ЎПB=ЎПE C. EF=BC D. EFЎОBC
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁ7·ЦЈ©ДіЦРС§1000ГыС§ЙъІОјУБЛЎұ»·ұЈЦӘК¶ҫәИьЎ°Ј¬ОӘБЛБЛҪвұҫҙОҫәИьіЙјЁЗйҝцЈ¬ҙУЦРійИЎБЛІҝ·ЦС§ЙъөДіЙјЁЈЁөГ·ЦИЎХыКэЈ¬Въ·ЦОӘ100·ЦЈ©ЧчОӘСщұҫҪшРРНіјЖЈ¬ІўЦЖЧчБЛИзНјЖөКэ·ЦІјұнәНЖөКэ·ЦІјЦұ·ҪНјЈЁІ»НкХыЗТҫЦІҝОЫЛрЈ¬ЖдЦРЎ°ЎцЎұұнКҫұ»ОЫЛрөДКэҫЭЈ©Ј®ЗлҪвҙрПВБРОКМвЈә
іЙјЁ·ЦЧй | ЖөКэ | ЖөВК |
50ЎЬxЈј60 | 8 | 0.16 |
60ЎЬxЈј70 | 12 | a |
70ЎЬxЈј80 | Ўц | 0.5 |
80ЎЬxЈј90 | 3 | 0.06 |
90ЎЬxЎЬ100 | b | c |
әПјЖ | Ўц | 1 |
ЈЁ1Ј©РҙіцaЈ¬bЈ¬cөДЦөЈ»
ЈЁ2Ј©Зл№АјЖХв1000ГыС§ЙъЦРУР¶аЙЩИЛөДҫәИьіЙјЁІ»өНУЪ70·ЦЈ»
ЈЁ3Ј©ФЪСЎИЎөДСщұҫЦРЈ¬ҙУҫәИьіЙјЁКЗ80·ЦТФЙПЈЁә¬80·ЦЈ©өДН¬С§ЦРЛж»ъійИЎБҪГыН¬С§ІОјУ»·ұЈЦӘК¶Рыҙ«»о¶ҜЈ¬ЗуЛщійИЎөД2ГыН¬С§АҙЧФН¬Т»ЧйөДёЕВКЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Ўч ABCЦРЈ¬ЎП ABCЈҪ90ЎгЈ¬ABЈҪBCЈ¬DФЪұЯ ACЙПЈ¬AE©Ш BDУЪ EЈ®
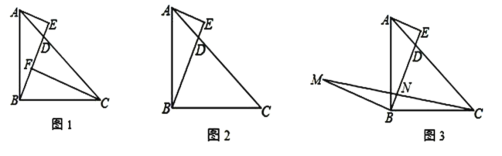
(1) ИзНј 1Ј¬Чч CFЎН BDУЪ FЈ¬ЗуЦӨЈәCFЈӯAEЈҪEFЈ»
(2) ИзНј 2Ј¬Иф BCЈҪCDЈ¬ЗуЦӨЈәBD=2AE Ј»
(3) ИзНј3Ј¬Чч BM ЎНBEЈ¬ЗТ BMЈҪBEЈ¬AEЈҪ2Ј¬ENЈҪ4Ј¬Б¬ҪУ CMҪ» BEУЪ NЈ¬ЗлЦұҪУРҙіцЎчBCMөДГж»эОӘ______Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪABCDЦРЈ¬ACУлBDҪ»УЪөгMЈ¬өгFФЪADЙПЈ¬AF=6cmЈ¬BF=12cmЈ¬ЎПFBM=ЎПCBMЈ¬өгEКЗBCөДЦРөгЈ¬ИфөгPТФ1cm/sГлөДЛЩ¶ИҙУөгAіц·ўЈ¬СШADПтөгFФЛ¶ҜЈ»өгQН¬КұТФ2cm/ГлөДЛЩ¶ИҙУөгCіц·ўЈ¬СШCBПтөгBФЛ¶ҜЈ¬өгPФЛ¶ҜөҪFөгКұНЈЦ№ФЛ¶ҜЈ¬өгQТІН¬КұНЈЦ№ФЛ¶ҜЈ¬өұөгPФЛ¶Ҝ__ГлКұЈ¬ТФPЎўQЎўEЎўFОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com