
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 计算“
计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 小颖说:“根据实验,一次实验中出现
小颖说:“根据实验,一次实验中出现![]() 点朝上的概率最大”;小红说:“如果投掷
点朝上的概率最大”;小红说:“如果投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
![]() 小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.
【答案】![]() “
“![]() 点朝上”出现的频率是
点朝上”出现的频率是![]() ;(2)小颖的说法是错误的,理由见解析;(3)
;(2)小颖的说法是错误的,理由见解析;(3)![]() (点数之和为
(点数之和为![]() 的倍数)
的倍数)![]() .
.
【解析】
列举出符合题意的各种情况的个数,再根据概率公式解答即可.注意概率在0和1之间的事件为随机事件.
解:![]() “
“![]() 点朝上”出现的频率是
点朝上”出现的频率是![]() ,
,
“![]() 点朝上”出现的频率是
点朝上”出现的频率是![]() ;
;![]() 小颖的说法是错误的.这是因为:“
小颖的说法是错误的.这是因为:“![]() 点朝上”的频率最大并不能说明“
点朝上”的频率最大并不能说明“![]() 点朝上”这一事件发生的概率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近;
点朝上”这一事件发生的概率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近;
小红的判断是错误的,因为事件发生具有随机性,故“![]() 点朝上”的次数不一定是
点朝上”的次数不一定是![]() 次;
次;![]() 列表如下:
列表如下:
小红投掷的点数小颖投掷的点数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∵点数之和为![]() 的倍数的一共有
的倍数的一共有![]() 种情况,总数有
种情况,总数有![]() 种情况,
种情况,
∴![]() (点数之和为
(点数之和为![]() 的倍数)
的倍数)![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
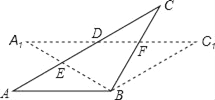
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时开始移动,点
同时开始移动,点![]() 的速度为
的速度为![]() 秒,点
秒,点![]() 的速度为
的速度为![]() 秒,点
秒,点![]() 移动到点
移动到点![]() 后停止,点
后停止,点![]() 也随之停止运动.下列时间瞬间中,能使
也随之停止运动.下列时间瞬间中,能使![]() 的面积为
的面积为![]() 的是( )
的是( )
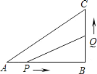
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋有![]() 个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了
个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了![]() 次,其中
次,其中![]() 次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角△ABC中,∠C=90°,∠A=30°,AB=4,以AC为腰,在△ABC外作顶角为30°的等腰三角形ACD,连接BD.请画出图形,并直接写出△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC,△MAD中,∠BAC=∠DMA=90°,连接BM,CD.且B,M,D三点共线

(1)当点D,点M在BC边下方,CD<BD时,如图①,求证:BM+CD=AM;(提示:延长DB到点N,使MN=MD,连接AN.)
(2)当点D在AC边右侧,点M在△ABC内部时,如图②;当点D在AB边左侧,点M在△ABC外部时,如图③,请直接写出线段BM,CD,AM之间的数量关系,不需要证明;
(3)在(1),(2)条件下,点E是AB中点,MF是△AMD的角平分线,连接EF,若EF=2MF=6,则CD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-5,5),(-2,3).

(1)请在图中的网格平面内画出平面直角坐标系xOy;
(2)请画出△ABC关于y轴对称的△A1B1C1,并写出顶点A1,B1,C1的坐标
(3)请在x轴上求作一点P,使△PB1C的周长最小.请标出点P的位置(保留作图痕迹,不需说明作图方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45°.
(1)试判断△ABD与△DCE是否相似并说明理由;
(2)设BD=x,AE=y,求y关于x的函数关系式;并指出当点D在BC上运动(不与B、C重合)时,AE是否存在最小值?若存在,求出最小值;若不存在,说明理由;
(3)当△ADE是等腰三角形时,求AE的长.
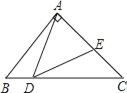
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com