
【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
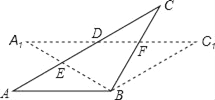
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
【答案】C
【解析】
①两个不同的三角形中有两个角相等,那么第三个角也相等;
②根据ASA进而得出△A1BF≌△CBE,即可得出A1E=CF;
③∠CDF=α,而∠C与顺时针旋转的度数不一定相等,所以DF与FC不一定相等;
④AE不一定等于CD,则AD不一定等于CE,
⑤用角角边可证明△A1BF≌△CBE后可得A1F=CE.
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴∠CBC1=α,∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠CBC1=α,故①正确,
∵AB=BC,
∴∠A=∠C,
∴∠C=∠A1
在△A1BF和△CBE中,
∠C=∠A1,A1B=BC,∠A1BF=∠CBE,
∴△A1BF≌△CBE,
∴BE=BF,A1F=CE,故⑤正确,
∵A1B=BC,
∴A1B-BE=BC-BF,即A1E=CF,故②正确,
∵∠CDF=α,α是可变化的角,∠C是固定角,
∴∠CDF不一定等于∠C,
∴DF不一定等于CF,故③错误,
∵AE不一定等于CD,
∴AD不一定等于CE,故④错误.
综上所述:①②⑤正确,
故选C.


科目:初中数学 来源: 题型:
【题目】《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”(译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?)若买得公鸡和母鸡之和不超过20只,且买得公鸡数不低于母鸡数,则此时买得小鸡_____只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以斜边
,以斜边![]() 的中点
的中点![]() 为旋转中心,把这个三角形按逆时针方向旋转
为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转后两个直角三角形重叠部分的面积为( )
,则旋转后两个直角三角形重叠部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
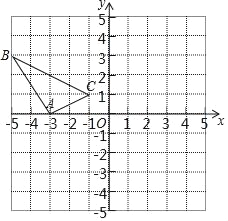
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某公园为迎接“中国–南亚博览会”设置的一休闲区.![]() ,弧
,弧![]() 的半径
的半径![]() 长是
长是![]() 米,
米,![]() 是
是![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,
上,![]() ,则图中休闲区(阴影部分)的面积是( )
,则图中休闲区(阴影部分)的面积是( )

A. ![]() 米
米![]() B.
B. ![]() 米
米![]() C.
C. ![]() 米
米![]() D.
D. ![]() 米
米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 计算“
计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 小颖说:“根据实验,一次实验中出现
小颖说:“根据实验,一次实验中出现![]() 点朝上的概率最大”;小红说:“如果投掷
点朝上的概率最大”;小红说:“如果投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
![]() 小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com