
ЁОЬтФПЁПЕШбќжБНЧЁїABCЃЌЁїMADжаЃЌЁЯBAC=ЁЯDMA=90ЁуЃЌСЌНгBMЃЌCDЃЎЧвBЃЌMЃЌDШ§ЕуЙВЯп

ЃЈ1ЃЉЕБЕуDЃЌЕуMдкBCБпЯТЗНЃЌCDЃМBDЪБЃЌШчЭМЂйЃЌЧѓжЄЃКBM+CD=AMЃЛЃЈЬсЪОЃКбгГЄDBЕНЕуNЃЌЪЙMN=MDЃЌСЌНгANЃЎЃЉ
ЃЈ2ЃЉЕБЕуDдкACБпгвВрЃЌЕуMдкЁїABCФкВПЪБЃЌШчЭМЂкЃЛЕБЕуDдкABБпзѓВрЃЌЕуMдкЁїABCЭтВПЪБЃЌШчЭМЂлЃЌЧыжБНгаДГіЯпЖЮBMЃЌCDЃЌAMжЎМфЕФЪ§СПЙиЯЕЃЌВЛашвЊжЄУїЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЃЌЃЈ2ЃЉЬѕМўЯТЃЌЕуEЪЧABжаЕуЃЌMFЪЧЁїAMDЕФНЧЦНЗжЯпЃЌСЌНгEFЃЌШєEF=2MF=6ЃЌдђCD=ЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЈ2ЃЉЕБЕуDдкACБпгвВрЃЌЕуMдкЁїABCФкВПЪБЃЌBM=CD+AMЃЈ3ЃЉ12-6![]()
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄDBЕНЕуNЃЌЪЙMN=MDЃЌгЩЬтвтПЩжЄЁїANDЪЧЕШбќжБНЧШ§НЧаЮЃЌПЩЕУЁЯNAD=ЁЯBAC=90ЁуЃЌAN=ADЃЌМДПЩжЄЁїABNЁеЁїACDЃЌПЩЕУBN=CDЃЌдђНсТлПЩЕУЃЎ
ЃЈ2ЃЉЕБЕуDдкACБпгвВрЃЌЕуMдкЁїABCФкВПЪБЃЌЃКдкЯпЖЮBMЩЯНиШЁMN=DMЃЌгЩЬтвтПЩжЄЁїANDЪЧЕШбќжБНЧШ§НЧаЮЃЌПЩЕУЁЯNAD=ЁЯBAC=90ЁуЃЌAN=ADЃЌМДПЩжЄЁїABNЁеЁїACDЃЌПЩЕУBN=CDЃЌМДПЩЕУBM=CD+AMЃЌЕБЕуDдкABБпзѓВрЃЌЕуMдкЁїABCЭтВПЪБЃЌбгГЄDMЕНNЃЌЪЙMN=DMЃЎгЩЬтвтПЩжЄЁїANDЪЧЕШбќжБНЧШ§НЧаЮЃЌПЩЕУЁЯNAD=ЁЯBAC=90ЁуЃЌAN=ADЃЌМДПЩжЄЁїABNЁеЁїACDЃЌПЩЕУBN=CDЃЌМДПЩЕУCD=BM+AM
ЃЈ3ЃЉгЩЬтвтПЩЕУEFЪЧжаЮЛЯпЃЌЗжРрЬжТлЃЌДњШыЙиЯЕЪНПЩЧѓCDЕФГЄЖШЃЎ
ЃЈ1ЃЉбгГЄDBЕНЕуNЃЌЪЙMN=MDЃЌСЌНгAN,
ЁпЕШбќжБНЧЁїABCЃЌЁїMAD,
ЁрAM=MDЃЌAB=ACЃЌЁЯADM=45Ёу=ЁЯMAD,
ЁпMN=MDЃЌЁЯDMA=90ЁуЃЌAM=AM,
ЁрЁїAMNЁеЁїAMD,
ЁрAD=ANЃЌЁЯNAM=ЁЯMAD=45Ёу,
ЁрЁЯNAD=90Ёу,
ЁпЁЯNAD=ЁЯBAC=90Ёу,
ЁрЁЯNAB=ЁЯCADЃЌЧвAN=ADЃЌAB=AC,
ЁрЁїABNЁеЁїACD,
ЁрBN=CD,
ЁпMN=BM+BN,
ЁрAM=MD=BM+CD,
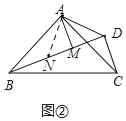
ЃЈ2ЃЉЕБЕуDдкACБпгвВрЃЌЕуMдкЁїABCФкВПЪБЃЌBM=CD+AM,
ШчЭМЃКдкЯпЖЮBMЩЯНиШЁMN=DM,
ЁпЕШбќжБНЧЁїABCЃЌЁїMAD,
ЁрAM=MDЃЌAB=ACЃЌЁЯADM=45Ёу=ЁЯMAD,
ЁпMN=DM,
ЁрAM=DM=MNЃЌЧвЁЯAMD=90Ёу,
ЁрЁЯAND=ЁЯADN=ЁЯNAM=ЁЯDAM=45Ёу,
ЁрAN=ADЃЌЁЯNAD=90Ёу,
ЁпЁЯNAD=ЁЯBAC=90Ёу,
ЁрЁЯBAN=ЁЯDACЃЌЧвAN=ADЃЌAB=AC,
ЁрЁїABNЁеЁїACD,
ЁрBN=CD,
ЁпBM=BN+MN,
ЁрBM=CD+AM,
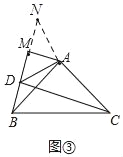
ЕБЕуDдкABБпзѓВрЃЌЕуMдкЁїABCЭтВПЪБЃЌCD=BM+AM,
ШчЭМЃКбгГЄDMЕНNЃЌЪЙMN=DMЃЎ
ЁпЕШбќжБНЧЁїABCЃЌЁїMAD,
ЁрAM=MDЃЌAB=ACЃЌЁЯADM=45Ёу=ЁЯMAD,
ЁпMN=DM,
ЁрAM=DM=MNЃЌЧвЁЯAMD=90Ёу,
ЁрЁЯAND=ЁЯADN=ЁЯNAM=ЁЯDAM=45Ёу,
ЁрAN=ADЃЌЁЯNAD=90Ёу,
ЁпЁЯNAD=ЁЯBAC=90Ёу,
ЁрЁЯBAN=ЁЯDACЃЌЧвAN=ADЃЌAB=AC,
ЁрЁїABNЁеЁїACD,
ЁрBN=CD,
ЁпBN=BM+MN,
ЁрCD=BM+AM,
ЃЈ3ЃЉЁпMFЪЧЁїAMDЕФНЧЦНЗжЯпЃЌЁЯDMA=90ЁуЃЌAM=DM,
ЁрAF=DF=MFЧвЕуEЪЧABжаЕу,
ЁрBD=2EF=12ЃЌ
ЁпEF=2MF=6,
ЁрMF=3,
ЁрAF=DF=MF=3,
ЁрAM=DM=3![]() ,
,
ЕБЕуDЃЌЕуMдкBCБпЯТЗНЃЌCDЃМBDЪБЃЌAM=BM+CD,
ЁрCD=3![]() ЉЃЈ12Љ3
ЉЃЈ12Љ3![]() ЃЉ=6
ЃЉ=6![]() Љ12ЃМ0,
Љ12ЃМ0,
ЙЪВЛДцдкетбљЕФЕуD,
ЕБЕуDдкABБпзѓВрЃЌЕуMдкЁїABCЭтВПЪБЃЌBM=CD+AM,
ЁрCD=BMЉAM=12Љ6![]() ,
,
ЕБЕуDдкABБпзѓВрЃЌЕуMдкЁїABCЭтВПЪБЃЌCD=BM+AM,
ЁпABЃМDM,
ЁрВЛДцдкетбљЕФЕуD,
злЩЯЫљЪіЃЌCD=12Љ6![]() ,
,
ЙЪД№АИЮЊ12Љ6![]() .
.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЪЧФГЙЋдАЮЊгНгЁАжаЙњЈCФЯбЧВЉРРЛсЁБЩшжУЕФвЛанЯаЧјЃЎ![]() ЃЌЛЁ
ЃЌЛЁ![]() ЕФАыОЖ
ЕФАыОЖ![]() ГЄЪЧ
ГЄЪЧ![]() УзЃЌ
УзЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкЛЁ
дкЛЁ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌдђЭМжаанЯаЧјЃЈвѕгАВПЗжЃЉЕФУцЛ§ЪЧЃЈ ЃЉ
ЃЌдђЭМжаанЯаЧјЃЈвѕгАВПЗжЃЉЕФУцЛ§ЪЧЃЈ ЃЉ

A. ![]() Уз
Уз![]() B.
B. ![]() Уз
Уз![]() C.
C. ![]() Уз
Уз![]() D.
D. ![]() Уз
Уз![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРЯЭѕЕФгуЬСРяФъГѕбјСЫФГжжгу2000ЬѕЃЌЕНФъЕзВЖРЬГіЪлЃЌЮЊСЫЙРМЦгуЕФзмВњСПЃЌДггуЬСРяВЖРЬСЫШ§ДЮЃЌЕУЕНШчЯТБэЕФЪ§ОнЃК
гуЕФЬѕЪ§ | ЦНОљУПЬѕгуЕФжЪСП | |
ЕквЛДЮВЖРЬ | 10 | 1.7ЧЇПЫ |
ЕкЖўДЮВЖРЬ | 25 | 1.8ЧЇПЫ |
ЕкШ§ДЮВЖРЬ | 15 | 2.0ЧЇПЫ |
ШєРЯЭѕЗХбјетжжгуЕФГЩЛюТЪЪЧ95%ЃЌдђЃК
(1)гуЬСРяетжжгуЦНОљУПЬѕжидМЖрЩйЧЇПЫЃП
(2)гуЬСРяетжжгуЕФзмВњСПЪЧЖрЩйЧЇПЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁгБКЭаЁКьСНЮЛЭЌбЇдкбЇЯАЁАИХТЪЁБЪБЃЌзіЭЖжРїЛзгЃЈжЪЕиОљдШЕФе§ЗНЬхЃЉЪЕбщЃЌЫћУЧЙВзіСЫ![]() ДЮЪЕбщЃЌЪЕбщЕФНсЙћШчЯТЃК
ДЮЪЕбщЃЌЪЕбщЕФНсЙћШчЯТЃК
ГЏЩЯЕФЕуЪ§ |
|
|
|
|
|
|
ГіЯжЕФДЮЪ§ |
|
|
|
|
|
|
![]() МЦЫуЁА
МЦЫуЁА![]() ЕуГЏЩЯЁБЕФЦЕТЪКЭЁА
ЕуГЏЩЯЁБЕФЦЕТЪКЭЁА![]() ЕуГЏЩЯЁБЕФЦЕТЪЃЎ
ЕуГЏЩЯЁБЕФЦЕТЪЃЎ
![]() аЁгБЫЕЃКЁАИљОнЪЕбщЃЌвЛДЮЪЕбщжаГіЯж
аЁгБЫЕЃКЁАИљОнЪЕбщЃЌвЛДЮЪЕбщжаГіЯж![]() ЕуГЏЩЯЕФИХТЪзюДѓЁБЃЛаЁКьЫЕЃКЁАШчЙћЭЖжР
ЕуГЏЩЯЕФИХТЪзюДѓЁБЃЛаЁКьЫЕЃКЁАШчЙћЭЖжР![]() ДЮЃЌФЧУДГіЯж
ДЮЃЌФЧУДГіЯж![]() ЕуГЏЩЯЕФДЮЪ§е§КУЪЧ
ЕуГЏЩЯЕФДЮЪ§е§КУЪЧ![]() ДЮЃЎЁБаЁгБКЭаЁКьЕФЫЕЗЈе§ШЗТ№ЃПЮЊЪВУДЃП
ДЮЃЎЁБаЁгБКЭаЁКьЕФЫЕЗЈе§ШЗТ№ЃПЮЊЪВУДЃП
![]() аЁгБКЭаЁКьИїЭЖжРвЛУЖїЛзгЃЌгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіСНУЖїЛзгГЏЩЯЕФЕуЪ§жЎКЭЮЊ
аЁгБКЭаЁКьИїЭЖжРвЛУЖїЛзгЃЌгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіСНУЖїЛзгГЏЩЯЕФЕуЪ§жЎКЭЮЊ![]() ЕФБЖЪ§ЕФИХТЪЃЎ
ЕФБЖЪ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТЭМЃЌвбжЊжБЯп![]() ЗжБ№гы
ЗжБ№гы![]() жсЃЌ
жсЃЌ![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌжБЯп
СНЕуЃЌжБЯп![]() ЃК
ЃК![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() СНЕуЕФзјБъЃЛ
СНЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуEЪЧЯпЖЮOBЕФжаЕуЃЌСЌНсAEЃЌЕуFЪЧЩфЯпOGЩЯвЛЕуЃЌ ЕБ![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШє![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЁЮ
ЁЮ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌДЫЪБдк
ЃЌДЫЪБдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌШєДцдкЃЌЧѓГіЕу
ЃЌШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
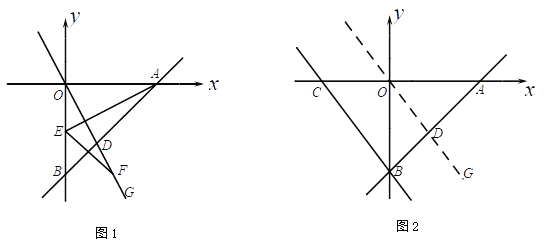
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈжЊЪЖБГОАЃЉ
ЮвУЧдкЕкЪЎвЛеТЁЖШ§НЧаЮЁЗжабЇЯАСЫШ§НЧаЮЕФБпгыНЧЕФаджЪЃЌдкЕкЪЎЖўеТЁЖШЋЕШШ§НЧаЮЁЗжабЇЯАСЫШЋЕШШ§НЧаЮЕФаджЪКЭХаЖЈЃЌдкЪЎШ§еТЁЖжсЖдГЦЁЗжабЇЯАСЫЕШбќШ§НЧаЮЕФаджЪКЭХаЖЈЃЎдквЛаЉЬНОПЬтжаОГЃгУвдЩЯжЊЪЖзЊЛЏНЧКЭБпЃЌНјЖјНтОіЮЪЬтЃЎ
1.ЃЈЮЪЬтГѕЬНЃЉ
ШчЭМЃЈ1ЃЉЃЌЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгADЃЌвдADЮЊвЛБпзїЁїADEЃЌЪЙЁЯDAEЃН90ЁуЃЌADЃНAEЃЌСЌНгBEЃЌВТЯыBEКЭCDгадѕбљЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ

2.ЃЈРрБШдйЬНЃЉ
ШчЭМЃЈ2ЃЉЃЌЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуMЪЧABЩЯвЛЕуЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгMDЃЌвдMDЮЊвЛБпзїЁїMDEЃЌЪЙЁЯDMEЃН90ЁуЃЌMDЃНMEЃЌСЌНгBEЃЌдђЁЯEBDЃН________ЃЎЃЈжБНгаДГіД№АИЃЌВЛаДЙ§ГЬЃЌЕЋвЊЧѓзїГіИЈжњЯпЃЉ
3.ЃЈЗНЗЈЧЈвЦЃЉ
ШчЭМЃЈ3ЃЉЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгADЃЌвдADЮЊвЛБпзїЕШБпШ§НЧаЮADEЃЌСЌНгBEЃЌдђBEЁЂBCжЎМфгадѕбљЕФЪ§СПЙиЯЕЃП________ЃЈжБНгаДГіД№АИЃЌВЛаДЙ§ГЬЃЉЃЎ
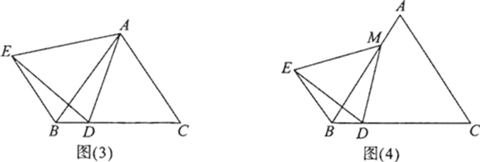
4.ЃЈЭиеЙДДаТЃЉ
ШчЭМЃЈ4ЃЉЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуMЪЧABЩЯвЛЕуЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгMDЃЌвдMDЮЊвЛБпзїЕШБпШ§НЧаЮMDEЃЌСЌНгBEЃЎВТЯыЁЯEBDЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАб![]() ЗХдкжБНЧзјБъЯЕФкЃЌЦфжа
ЗХдкжБНЧзјБъЯЕФкЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ

![]() Еу
Еу![]() ЕФзјБъЪЧ________ЃЛ
ЕФзјБъЪЧ________ЃЛ
![]() НЋ
НЋ![]() би
би![]() жсЯђгвЦНвЦЃЌЕБЕу
жсЯђгвЦНвЦЃЌЕБЕу![]() ТфдкжБЯп
ТфдкжБЯп![]() ЩЯЪБЃЌЯпЖЮ
ЩЯЪБЃЌЯпЖЮ![]() ЩЈЙ§ЕФУцЛ§ЮЊ________ЃЎ
ЩЈЙ§ЕФУцЛ§ЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕчЯпИЫЩЯЕФCДІв§РЯпCEЁЂCFЙЬЖЈЕчЯпИЫЃЌРЯпCEКЭЕиУцГЩ60ЁуНЧЃЌдкРыЕчЯпИЫ6УзЕФBДІАВжУВтНЧвЧЃЌдкAДІВтЕУЕчЯпИЫЩЯCДІЕФбіНЧЮЊ30ЁуЃЌвбжЊВтНЧвЧИпABЮЊ1.5УзЃЌЧѓРЯпCEЕФГЄЃЈНсЙћБЃСєИљКХЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ7ЗжЃЉФГжабЇ1000УћбЇЩњВЮМгСЫЁБЛЗБЃжЊЪЖОКШќЁАЃЌЮЊСЫСЫНтБОДЮОКШќГЩМЈЧщПіЃЌДгжаГщШЁСЫВПЗжбЇЩњЕФГЩМЈЃЈЕУЗжШЁећЪ§ЃЌТњЗжЮЊ100ЗжЃЉзїЮЊбљБОНјааЭГМЦЃЌВЂжЦзїСЫШчЭМЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЈВЛЭъећЧвОжВПЮлЫ№ЃЌЦфжаЁАЁіЁББэЪОБЛЮлЫ№ЕФЪ§ОнЃЉЃЎЧыНтД№ЯТСаЮЪЬтЃК
ГЩМЈЗжзщ | ЦЕЪ§ | ЦЕТЪ |
50ЁмxЃМ60 | 8 | 0.16 |
60ЁмxЃМ70 | 12 | a |
70ЁмxЃМ80 | Ёі | 0.5 |
80ЁмxЃМ90 | 3 | 0.06 |
90ЁмxЁм100 | b | c |
КЯМЦ | Ёі | 1 |
ЃЈ1ЃЉаДГіaЃЌbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉЧыЙРМЦет1000УћбЇЩњжагаЖрЩйШЫЕФОКШќГЩМЈВЛЕЭгк70ЗжЃЛ
ЃЈ3ЃЉдкбЁШЁЕФбљБОжаЃЌДгОКШќГЩМЈЪЧ80ЗжвдЩЯЃЈКЌ80ЗжЃЉЕФЭЌбЇжаЫцЛњГщШЁСНУћЭЌбЇВЮМгЛЗБЃжЊЪЖаћДЋЛюЖЏЃЌЧѓЫљГщШЁЕФ2УћЭЌбЇРДздЭЌвЛзщЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com