
【题目】如下图,已知直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() :
:![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)如图1,点E是线段OB的中点,连结AE,点F是射线OG上一点, 当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
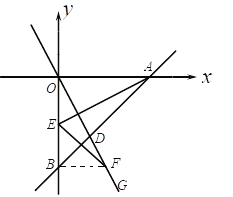
(3)如图2,若![]() ,过
,过![]() 点作
点作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,此时在
,此时在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
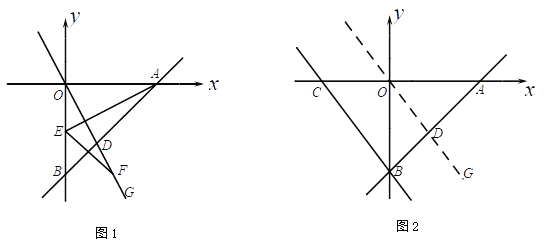
【答案】(1)A(4,0),B(0,-4)(2)EF=![]() (3)
(3)![]()
![]()
【解析】
(1)根据直线与坐标轴的坐标特点即可求解;
(2)连结BF,根据题意可证明△AOE≌△OBF,得到BF=OE,求出BF=2,再利用在Rt△BEF中,由勾股定理求得EF=![]() ;
;
(3)根据平行求出直线BC的函数表达式为 ![]() 得到C(-3,0),OC=3再分当M1在A点左侧,当M点在A点右侧分别进行求解.
得到C(-3,0),OC=3再分当M1在A点左侧,当M点在A点右侧分别进行求解.
(1) ![]() 直线
直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于A,B两点,
轴分别相交于A,B两点,
![]()
![]() 时,
时, ![]() ;
;![]() 时,
时,![]()
![]() A(4,0),B(0,-4).
A(4,0),B(0,-4).
(2)连结BF,由(1) ,得OA=OB,∠AOB=![]() ,
,
![]() ∠BOF+∠AOF=
∠BOF+∠AOF=![]() ,
,
![]() OF⊥AE,
OF⊥AE,
![]() ∠AOF+∠EAO=
∠AOF+∠EAO=![]() .
.
![]() ∠BOF=∠EAO,
∠BOF=∠EAO,
又![]() AE=OF,OA=OB,
AE=OF,OA=OB,
![]() △AOE≌△OBF.
△AOE≌△OBF.
![]() ∠OBF=∠AOE=
∠OBF=∠AOE=![]() ,BF=OE.
,BF=OE.
![]() E是OB的中点 ,
E是OB的中点 ,
![]() OE=
OE=![]() OB=2.
OB=2.
![]() BF=2.
BF=2.
在Rt△BEF中,由勾股定理,EF2=BF2+BE2=22+22=8.
又EF>0,
![]() EF=
EF=![]() .
.
(3)∵BC∥OG,![]()
∴直线BC的函数表达式为 ![]()
又B(0,-4),
∴![]() .
.
∴![]()
令![]()
得![]() .
.
即C(-3,0).
∴OC=3.
故①当M1在A点左侧,在OA上取OM1=3,则M1,C关于y轴对称.
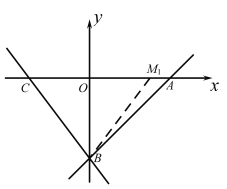
∴∠MBO=∠CBO.
∵OA=OB,∠AOB=90°,
∴∠ABO=45°.
而∠M1BO+∠ABM1=∠ABO=45°,
即∠CBO+∠ABM1=45°.
∴M1即为所求的点.
∴![]()
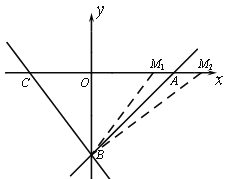
②当M点在A点右侧,满足∠CBO+∠ABM2=45°时,又∠ABO=45°,
∴∠CBM2=∠CBO+∠ABM2+∠ABO=45°+45°=90°.
设M2(m,0),
在Rt△CBM2与Rt△BOM2中,由勾股定理,得:
![]()
即![]()
∴![]()
∴![]()
∴![]()
![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )
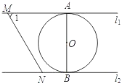
A. ![]() B. 若
B. 若![]() 与
与![]() 相切,则
相切,则![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D.
相切 D. ![]() 和
和![]() 的距离为
的距离为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “某篮球运动员投篮的命中率大约是82.3%”表示投篮1次,命中的可能性较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋有![]() 个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了
个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了![]() 次,其中
次,其中![]() 次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC如图放置,A(1,1),B(3,1),等边三角形的中心是点D,若将点D绕点A旋转90°后得到点D′,则D′的坐标( )
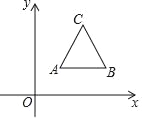
A. (1+![]() ,0) B. (1﹣
,0) B. (1﹣![]() ,0)或(1+
,0)或(1+![]() ,2)
,2)
C. (1+![]() ,0)或(1﹣
,0)或(1﹣![]() ,2) D. (2+
,2) D. (2+![]() ,0)或(2﹣
,0)或(2﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC,△MAD中,∠BAC=∠DMA=90°,连接BM,CD.且B,M,D三点共线

(1)当点D,点M在BC边下方,CD<BD时,如图①,求证:BM+CD=AM;(提示:延长DB到点N,使MN=MD,连接AN.)
(2)当点D在AC边右侧,点M在△ABC内部时,如图②;当点D在AB边左侧,点M在△ABC外部时,如图③,请直接写出线段BM,CD,AM之间的数量关系,不需要证明;
(3)在(1),(2)条件下,点E是AB中点,MF是△AMD的角平分线,连接EF,若EF=2MF=6,则CD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有10名工作人员他们的月工资情况如表(其中x为未知数),他们的月平均工资是2.3万元,根据表中信息计算该公司工作人员的月工资的中位数和众数分别是( )
职位 | 经理 | 副经理 | A职员 | B职员 | C职员 |
人数 | 1 | 2 | 2 | 4 | 1 |
月工资(万元/人) | 5 | 3 | 2 | x | 0.8 |
A. 2,4 B. 1.9,1.8 C. 2,1.8 D. 1.8,1.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx过点A(1,4)、B(﹣3,0),过点A作直线AC∥x轴,交抛物线于另一点C,在x轴上有一点D(4,0),连接CD.

(1)求抛物线的表达式;
(2)若在抛物线上存在点Q,使得CD平分∠ACQ,请求出点Q的坐标;
(3)在直线CD的下方的抛物线上取一点N,过点N作NG∥y轴交CD于点G,以NG为直径画圆在直线CD上截得弦GH,问弦GH的最大值是多少?
(4)一动点P从C点出发,以每秒1个单位长度的速度沿C﹣A﹣D运动,在线段CD上还有一动点M,问是否存在某一时刻使PM+AM=4?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com