
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
科目:初中数学 来源: 题型:
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 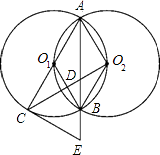
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P. 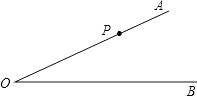
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示: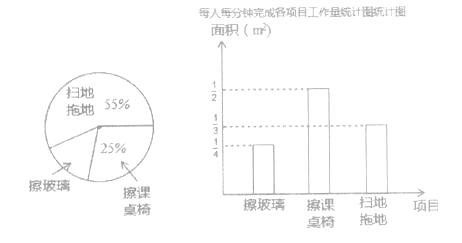
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅
m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
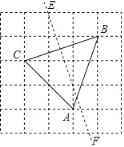
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D. 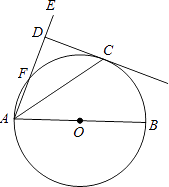
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半径;②求tan∠BAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com