
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 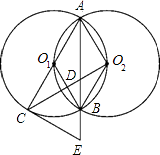
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
【答案】
(1)证明:∵⊙O1与⊙O2是等圆,
∴AO1=O1B=BO2=O2A,
∴四边形AO1BO2是菱形;
(2)证明:∵四边形AO1BO2是菱形,
∴∠O1AB=∠O2AB,
∵CE是⊙O1的切线,AC是⊙O1的直径,
∴∠ACE=∠AO2C=90°,
∴△ACE∽△AO2D,
![]() ,
,
即CE=2DO2;
(3)解:∵四边形AO1BO2是菱形,
∴AC∥BO2
∴△ACD∽△BO2D,
∴ ![]() ,
,
∴AD=2BD,
∵ ![]() ,
,
∴ ![]() ,
,

【解析】(1)根据⊙O1与⊙O2是等圆,可得AO1=O1B=BO2=O2A,利用四条边都相等的四边形是菱形可判定出结论;(2)根据已知得出△ACE∽△AO2D,进而得出 ![]() ,即可得出答案;(3)首先证明△ACD∽△BO2D,得出
,即可得出答案;(3)首先证明△ACD∽△BO2D,得出 ![]() ,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
【考点精析】掌握菱形的判定方法和相交两圆的性质是解答本题的根本,需要知道任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;相交的两个圆的连心线垂直平分两圆的公共弦.


科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4, ①
所以c2(a2-b2)=( a2-b2)( a2+b2). ②
所以c2= a2+b2. ③
所以△ABC是直角三角形. ④
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代码为 ;
(2)错误的原因为 ;
(3)请你将正确的解答过程写下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动.设点P原来的速度为xcm/s.

(1)点Q的速度为 cm/s(用含x的代数式表示);
(2)求点P原来的速度.
(3)判断E点的位置并求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,且∠BAD=20°,∠E=30°,则∠B的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂分别安排甲乙两个车间加工1000个同一型号的奥运会吉祥物,每名工人每天加工吉祥物的个数相等且保持不变,由于生产需要,其中一个车间推迟两天开始加工,刚开始加工时,甲车间有10名工人,乙车间有12名工人,图中线段OB和折线ACB分别表示两个车间的加工情况.依据图中提供的信息,完成下列各题:
(1)线段OB反映的是 车间的加工情况;
(2)开始加工后,甲车间加工多少天后,两车间加工吉祥物数相同?
(3)根据折线段反映的加工情况,请你提出一个问题,并给出解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )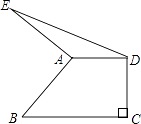
A.10
B.11
C.12
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).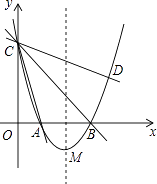
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com