
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )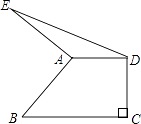
A.10
B.11
C.12
D.13
【答案】A
【解析】解:过A作AN⊥BC于N,过E作EM⊥AD,交DA延长线于M,
∵AD∥BC,∠C=90°,
∴∠C=∠ADC=∠ANC=90°,
∴四边形ANCD是矩形,
∴∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,
∴BN=9﹣5=4,
∵∠M=∠EAB=∠MAN=∠ANB=90°,
∴∠EAM+∠BAM=90°,∠MAB+∠NAB=90°,
∴∠EAM=∠NAB,
∵在△EAM和△BAN中,  ,
,
∴△EAM≌△BAN(AAS),
∴EM=BN=4,
∴△ADE的面积是 ![]() ×AD×EM=
×AD×EM= ![]() ×5×4=10.
×5×4=10.
故选A.
过A作AN⊥BC于N,过E作EM⊥AD,交DA延长线于M,得出四边形ANCD是矩形,推出∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,求出BN=4,求出∠EAM=∠NAB,证△EAM≌△BAN,求出EM=BN=4,根据三角形的面积公式求出即可.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均匀分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于________;
(2)请你用两种不同的方法表示图②中阴影部分的面积,方法一:__________________,方法二:________________;
(3)观察图②,你能写出代数式(m+n)2,(m-n)2,mn之间的关系吗?
(4)应用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
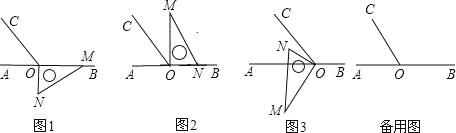
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 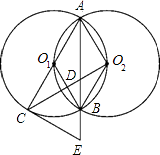
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:![]() =1÷4=0.25;
=1÷4=0.25;![]() =
=![]() =8÷5=1.6;
=8÷5=1.6;![]() =1÷3=
=1÷3=![]() ,反之,0.25=
,反之,0.25=![]() =
=![]() ;1.6=
;1.6=![]() =
=![]() =
=![]() .那么
.那么![]() ,
,![]() 怎么化成分数呢?
怎么化成分数呢?
解:∵![]() ×10=3+
×10=3+![]() , ∴不妨设
, ∴不妨设![]() =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x=![]() ,即
,即![]() =
=![]() ;
;
∵![]() =
=![]() ,设
,设![]() =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=![]() ,
,
∴![]() =
=![]() =1+x=1+
=1+x=1+![]() =
=![]()
⑴将分数化为小数:![]() =______,
=______,![]() =_______;
=_______;
⑵将小数化为分数:![]() =______,
=______,![]() =_______;
=_______;
⑶将小数![]() 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇左市江州区太平镇壶城社区调查居民双休日的学习状况,采取了下列调查方式;a:从崇左高中、太平镇中、太平小学三所学校中选取200名教师;b:从不同住宅楼(即江湾花园与万鹏住宅楼)中随机选取200名居民;c:选取所管辖区内学校的200名在校学生.并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图.以下结论:①上述调查方式最合理的是b;②在这次调查的200名教师中,在家学习的有60人;③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人;④小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是0.1.其中正确的结论是( ) 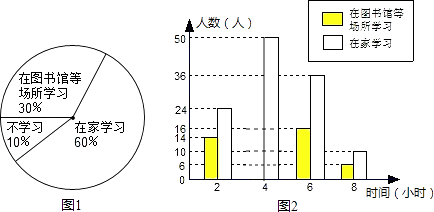
A.①④
B.②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com