
【题目】(1)计算: ![]()
(2)先化简,再求值:3a-2(a-ab)+(b-2ab),其中a,b满足|2a+b|+(2-b) =0
(3)解方程: ![]() .
.
【答案】(1)![]() ;(2) 5;(3) x=-12.
;(2) 5;(3) x=-12.
【解析】
(1)先计算乘方,然后进行括号内的乘法运算与减法运算,最后进行除法运算即可;
(2)先去括号,合并同类项,然后根据非负数的性质求出a、b的值代入进行计算即可;
(3)按去分母、去括号、移项、合并同类项、系数化为1的步骤进行求解即可.
(1)原式=(-9×![]() -0.8)÷(-
-0.8)÷(-![]() )
)
=(-1-0.8)×(-![]() )
)
=-![]() ×(-
×(-![]() )
)
=![]() ;
;
(2)原式=3a-2a+2ab+b-2ab=a+b,
由题意得,2a+b=0且2-b=0,
解得a=-1,b=2,
所以原式=(-1)+2=1+4=5;
(3)去分母,得3(x+2)=2(2x+3)+12,
去括号,得3x+6=4x+6+12,
移项,得3x-4x=6+12-6,
合并同类项,得-x=12,
系数化为1,得x=-12.


科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )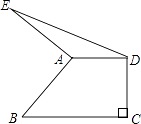
A.10
B.11
C.12
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C. 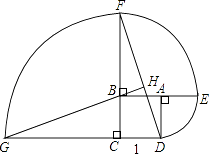
(1)求点D沿三条弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则PEF和PGH的面积和等于.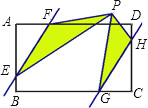
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,如果AB=AC,那么图中全等的三角形有( )
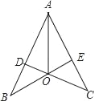
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+4m﹣2.
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
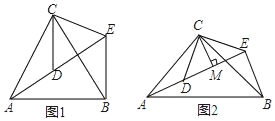
【题目】(1)问题探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
①求证:△CDA≌△CEB;
②求∠AEB的度数.
(2)问题变式:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①请求出∠AEB的度数
②直接写出线段AE、CM、BE之间的数量关系,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com