
【题目】如图,E,F分别是 □ABCD的边AB,CD的中点,则图中平行四边形的个数共有( ).
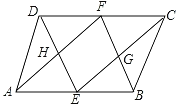
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
首先根据四边形ABCD是平行四边形,可得DC∥AB,DC=AB,再根据E、F分别是边AB、CD的中点,可得DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,进而可根据一组对边平行且相等的四边形是平行四边形证明四边形DFBE和CFAE都是平行四边形,再根据平行四边形的性质可得DE∥FB,AF∥CE,进而可证出四边形FHEG是平行四边形。
AB,进而可根据一组对边平行且相等的四边形是平行四边形证明四边形DFBE和CFAE都是平行四边形,再根据平行四边形的性质可得DE∥FB,AF∥CE,进而可证出四边形FHEG是平行四边形。
解:∵四边形ABCD是平行四边形,
 ∴DC∥AB,DC=AB,
∴DC∥AB,DC=AB,
∵E、F分别是边AB、CD的中点,
∴DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,
AB,
∵DC=AB,
∴DF=FC=AE=EB,
∴四边形DFBE和CFAE都是平行四边形,
∴DE∥FB,AF∥CE,
∴四边形FHEG是平行四边形,
故选C。


科目:初中数学 来源: 题型:
【题目】将一次函数y=kx+4(k≠0)的图象称为直线l.
(1)若直线l经过点(2,0),直接写出关于x的不等式kx+4>0的解集;
(2)若直线l经过点(3,﹣2),求这个函数的表达式;
(3)若将直线l向右平移2个单位长度后经过点(5,5),求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D. 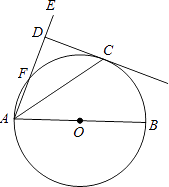
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半径;②求tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年法国网球公开赛中,我国选手李娜在决赛中成功击败对手夺冠,称为获得法国网球公开赛冠军的亚洲第一人.某班体育委员就本班同学对该届法国网球公开赛的了解程度进行全面调查统计,收集数据后绘制了两幅不完整的统计图,如图(1)和图(2).根据图中的信息,解答下列问题: 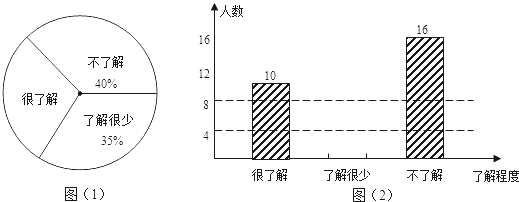
(1)该班共有名学生;
(2)在图(1)中,“很了解”所对应的圆心角的度数为;
(3)把图(2)中的条形图形补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。
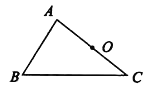
小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.
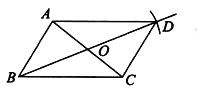
所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com