
【题目】已知关于x的一次函数y=mx+4m﹣2.
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标.
【答案】(1)m=![]() ;(2)m≥;
;(2)m≥;![]() (3)则不论m取何实数这个函数的图象都过定点(﹣4,﹣2).
(3)则不论m取何实数这个函数的图象都过定点(﹣4,﹣2).
【解析】
(1)直接把(0,0)代入求出m的值即可;
(2)根据一次函数的性质列出关于m的不等式组,求出m的取值范围即可;
(3)把一次函数解析式化为关于m的一元一次方程,根据方程有无数解解答.
解:(1)∵这个函数的图象经过原点,
∴当x=0时,y=0,即4m﹣2=0,
解得m=![]() ;
;
(2)∵这个函数的图象不经过第四象限,
∴![]()
解得,m≥![]() ;
;
(3)一次函数y=mx+4m﹣2变形为:m(x+4)=y+2,
∵不论m取何实数这个函数的图象都过定点,
∴x+4=0,y+2=0,
解得,x=﹣4,y=﹣2,
则不论m取何实数这个函数的图象都过定点(﹣4,﹣2).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
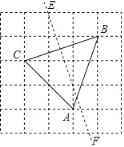
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在横线上填写合适的内容,完成下面的证明:
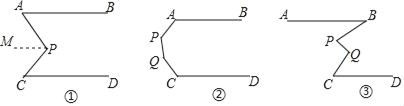
(1)如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB,
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以PM∥CD( )
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C( )
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。
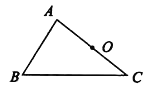
小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.
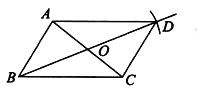
所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com