
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
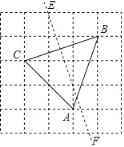
【答案】②③④.
【解析】
根据勾股定理求出AC、BC、AB长,即可判断①和②,求出AC边上的高,即可判断③,证△MTD≌△BZC,推出∠ZBC=∠TMD,能求出EF⊥BC,根据等腰三角形性质即可求出CO=BO,即可判断④.
∵由勾股定理得:AB=![]() =
=![]() ,AC=
,AC=![]() =2
=2![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AB=BC,∴△ABC的形状是等腰三角形,∴①错误;
△ABC的周长是![]() +
+![]() +2
+2![]() =2
=2![]() +2
+2![]() ,∴②正确;
,∴②正确;
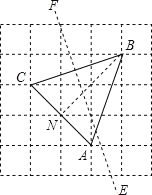
连接BN,由勾股定理得:AN=CN,
在△BCN和△BAN中
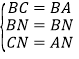 ∴△BCN≌△BAN,
∴△BCN≌△BAN,
∴∠BNC=∠BNA,
∵∠BNC+∠BNA=180![]() ,
,
∴∠BNC=90![]() ,
,
由勾股定理得:BN=![]() =2
=2![]() ,
,
∴△ABC的面积是![]() AC×BN=
AC×BN=![]() ×2
×2![]() ×2
×2![]() =4,∴③正确;
=4,∴③正确;
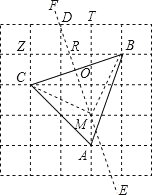
在△MTD和△BZC中
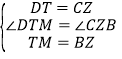 ∴△MTD≌△BZC,
∴△MTD≌△BZC,
∴∠ZBC=∠TMD,
∵∠MTD=90,
∴∠TDM+∠TMD=∠ZBC+∠BRO=90![]() ,
,
∴∠ROB=90![]() ,
,
∴EF⊥BC,
由勾股定理得:BM=CM,
∴CO=BO,即EF是线段BC的垂直平分线,∴④正确;
故答案为:②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=30°,则∠BOE=_______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为___________;
(2)当射线OE绕点O逆时针旋转到图2的位置时,(1)中∠BOE和∠COF的数量关系是否仍成立?请说明理由.
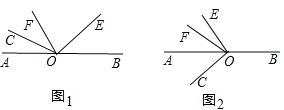
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+4m﹣2.
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.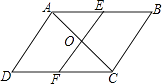
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com