
ΓΨΧβΡΩΓΩΘ®1Θ©Έ ΧβΧΫΨΩΘΚ»γΆΦ1Θ§ΓςACBΚΆΓςDCEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§Ν§Ϋ”BEΘ°
ΔΌ«σ÷ΛΘΚΓςCDAΓ’ΓςCEBΘΜ
ΔΎ«σΓœAEBΒΡΕ» ΐΘ°
Θ®2Θ©Έ Χβ±δ ΫΘΚ»γΆΦ2Θ§ΓςACBΚΆΓςDCEΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACB=ΓœDCE=90ΓψΘ§ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§CMΈΣΓςDCE÷–DE±Ώ…œΒΡΗΏΘ§Ν§Ϋ”BEΘ°
ΔΌ«κ«σ≥ωΓœAEBΒΡΕ» ΐ
ΔΎ÷±Ϋ”–¥≥ωœΏΕΈAEΓΔCMΓΔBE÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Μ±ΊΥΒΟςάμ”…Θ°
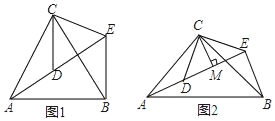
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ÷ΛΟςΦϊΫβΈωΘΜΔΎ60ΓψΘΜΘ®2Θ©ΔΌ90ΓψΘΜΔΎAE= BE+2CM
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫCA=CB=ABΘ§CD=CE=DEΘ§ΓœACB=ΓœDCE=60ΓψΘ§άϊ”ΟSASΕ®άμ÷ΛΟςΓςCDAΓ’ΓςCEBΘΜ
ΔΎΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœCEB=ΓœADC=120ΓψΘ§ΫαΚœΆΦ–ΈΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©ΔΌΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫCA=CBΘ§CD=CEΘ§ΓœACD=ΓœBCEΘ§άϊ”ΟSASΕ®άμ÷ΛΟςΓςCDAΓ’ΓςCEBΘ§άϊ”Ο»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΦΤΥψΦ¥Ω…ΘΜ
ΔΎΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫBE=ADΘ§ΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫDE=2CMΘ§ΫαΚœΆΦ–ΈΫβ¥πΘ°
Θ®1Θ©ΔΌ÷ΛΟςΘΚΓΏΓςACBΚΆΓςDCEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύCA=CB=ABΘ§CD=CE=DEΘ§ΓœACB=ΓœDCE=60ΓψΘ§
ΓύΓœACB©¹ΓœDCB=ΓœDCE©¹ΓœDCBΘ§Φ¥ΓœACD=ΓœBCEΘ§
‘ΎΓςCDAΚΆΓςCEB÷–Θ§
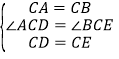 Θ§
Θ§
ΓύΓςCDAΓ’ΓςCEBΘΜ
ΔΎΫβΘΚΓΏΓœCDE=60ΓψΘ§
ΓύΓœADC=120ΓψΘ§
ΓΏΓςCDAΓ’ΓςCEBΘ§
ΓύΓœCEB=ΓœADC=120ΓψΘ§
ΓύΓœAEB=120Γψ©¹60Γψ=60ΓψΘΜ
Θ®2Θ©ΔΌΓΏΓςACBΚΆΓςDCEΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACB=ΓœDCE=90ΓψΘ§
ΓύCA=CBΘ§CD=CEΘ§ΓœACB©¹ΓœDCB=ΓœDCE©¹DCBΘ§Φ¥ΓœACD=ΓœBCEΘ§
‘ΎΓςCDAΚΆΓςCEB÷–Θ§
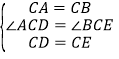 Θ§
Θ§
ΓύΓςCDAΓ’ΓςCEBΘ§
ΓύΓœCEB=ΓœADC=135ΓψΘ§
ΓύΓœAEB=135Γψ©¹45Γψ=90ΓψΘΜ
ΔΎΫβΘΚΓΏΓςCDAΓ’ΓςCEBΘ§
ΓύBE=ADΘ§
ÿCD=CEȧCMâDEȧ
ΓύDM=MEΘ§”÷ΓœDCE=90ΓψΘ§
ΓύDE=2CMΘ§
ΓύAE=AD+DE=BE+2CMΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≥γΉσ –Ϋ≠÷ί«χΧΪΤΫ’ρΚχ≥«…γ«χΒς≤ιΨ”ΟώΥΪ–ί»’ΒΡ―ßœΑΉ¥ΩωΘ§≤…»ΓΝΥœ¬Ν–Βς≤ιΖΫ ΫΘΜaΘΚ¥”≥γΉσΗΏ÷–ΓΔΧΪΤΫ’ρ÷–ΓΔΧΪΤΫ–Γ―ß»ΐΥυ―ß–Θ÷–―Γ»Γ200ΟϊΫΧ ΠΘΜbΘΚ¥”≤ΜΆ§ΉΓ’§¬ΞΘ®Φ¥Ϋ≠ΆεΜ®‘Α”κΆρ≈τΉΓ’§¬ΞΘ©÷–ΥφΜζ―Γ»Γ200ΟϊΨ”ΟώΘΜcΘΚ―Γ»ΓΥυΙήœΫ«χΡΎ―ß–ΘΒΡ200Οϊ‘Ύ–Θ―ß…ζΘ°≤ΔΫΪΉνΚœάμΒΡΒς≤ιΖΫ ΫΒΟΒΫΒΡ ΐΨί÷Τ≥……»–ΈΆ≥ΦΤΆΦΚΆ≤ΩΖ÷ ΐΨίΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ°“‘œ¬Ϋα¬έΘΚΔΌ…œ ωΒς≤ιΖΫ ΫΉνΚœάμΒΡ «bΘΜΔΎ‘Ύ’β¥ΈΒς≤ιΒΡ200ΟϊΫΧ Π÷–Θ§‘ΎΦ“―ßœΑΒΡ”–60»ΥΘΜΔέΙάΦΤΗΟ…γ«χ2000ΟϊΨ”Οώ÷–ΥΪ–ί»’―ßœΑ ±Φδ≤Μ…Ό”Ύ4–Γ ±ΒΡ»Υ ΐ «1180»ΥΘΜΔή–ΓΟςΒΡ ε εΉΓ‘ΎΗΟ…γ«χΘ§Ρ«Ο¥ΥΪ–ί»’Υϊ»Ξ ε εΦ“ ±Θ§’ΐΚΟ ε ε≤Μ―ßœΑΒΡΗ≈¬ «0.1Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ «Θ®ΓΓΓΓΘ© 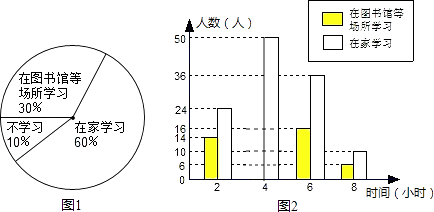
A.ΔΌΔή
B.ΔΎΔή
C.ΔΌΔέΔή
D.ΔΌΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ(1)ΦΤΥψ: ![]()
(2)œ»Μ·Φρ,‘Ό«σ÷Β:3a-2(a-ab)+(b-2ab),Τδ÷–a,b¬ζΉψ|2a+b|+(2-b) =0
(3)ΫβΖΫ≥Χ: ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«κ‘ΎΚαœΏ…œΧν–¥Κœ ΒΡΡΎ»ίΘ§Άξ≥…œ¬ΟφΒΡ÷ΛΟςΘΚ
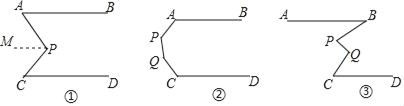
Θ®1Θ©»γΆΦΔΌ»γΙϊABΓΈCDΘ§«σ÷ΛΘΚΓœAPCΘΫΓœA+ΓœCΘ°
÷ΛΟςΘΚΙΐPΉςPMΓΈABΘ§
Υυ“‘ΓœAΘΫΓœAPMΘ§Θ®ΓΓ ΓΓΘ©
“ρΈΣPMΓΈABΘ§ABΓΈCDΘ®“―÷ΣΘ©
Υυ“‘PMΓΈCDΘ®ΓΓ ΓΓΘ©
Υυ“‘ΓœCΘΫΓΓ ΓΓΘ®ΓΓ ΓΓΘ©
“ρΈΣΓœAPCΘΫΓœAPM+ΓœCPM
Υυ“‘ΓœAPCΘΫΓœA+ΓœCΘ®ΓΓ ΓΓΘ©
Θ®2Θ©»γΆΦΔΎΘ§ABΓΈCDΘ§ΗυΨί…œΟφΒΡΆΤάμΖΫΖ®Θ§÷±Ϋ”–¥≥ωΓœA+ΓœP+ΓœQ+ΓœCΘΫΓΓ ΓΓΘ°
Θ®3Θ©»γΆΦΔέΘ§ABΓΈCDΘ§»τΓœABPΘΫxΘ§ΓœBPQΘΫyΘ§ΓœPQCΘΫzΘ§ΓœQCDΘΫmΘ§‘ρmΘΫΓΓ ΓΓΘ®”ΟxΓΔyΓΔz±μ ΨΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ“―÷ΣΝΫ÷±œΏΘ§L1ΘΚyΘΫk1x+b1Θ§L2ΘΚyΘΫk2x+b2Θ§
»τL1ΓΆL2Θ§‘ρ”–k1k2ΘΫ©¹1Θ§ΗυΨί“‘…œΫα¬έΫβ¥πœ¬Ν–ΗςΧβΘΚ
Θ®1Θ©“―÷Σ÷±œΏyΘΫ2x+1”κ÷±œΏyΘΫkx©¹1¥Ι÷±Θ§«σkΒΡ÷ΒΘΜ
Θ®2Θ©»τ“ΜΧθ÷±œΏΨ≠ΙΐAΘ®2Θ§3Θ©Θ§«“”κyΘΫ©¹![]() x+3¥Ι÷±Θ§«σ’βΧθ÷±œΏΥυΕ‘”ΠΒΡ“Μ¥ΈΚ· ΐΒΡΙΊœΒ ΫΘ°
x+3¥Ι÷±Θ§«σ’βΧθ÷±œΏΥυΕ‘”ΠΒΡ“Μ¥ΈΚ· ΐΒΡΙΊœΒ ΫΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
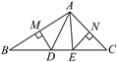
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ABΘ§ACΒΡ¥Ι÷±ΤΫΖ÷œΏΖ÷±πΫΜBC”ΎDΘ§EΝΫΒψΘ§¥ΙΉψΖ÷±π «MΘ§N.
(1)»τΓςADEΒΡ÷ή≥Λ «10Θ§«σBCΒΡ≥ΛΘΜ
(2)»τΓœBACΘΫ100ΓψΘ§«σΓœDAEΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪ“Μ¥ΈΚ· ΐy=kx+4Θ®kΓΌ0Θ©ΒΡΆΦœσ≥ΤΈΣ÷±œΏlΘ°
Θ®1Θ©»τ÷±œΏlΨ≠ΙΐΒψΘ®2Θ§0Θ©Θ§÷±Ϋ”–¥≥ωΙΊ”ΎxΒΡ≤ΜΒ» Ϋkx+4ΘΨ0ΒΡΫβΦ·ΘΜ
Θ®2Θ©»τ÷±œΏlΨ≠ΙΐΒψΘ®3Θ§©¹2Θ©Θ§«σ’βΗωΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®3Θ©»τΫΪ÷±œΏlœρ”“ΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»ΚσΨ≠ΙΐΒψΘ®5Θ§5Θ©Θ§«σkΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
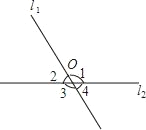
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§÷±œΏl1”κl2œύΫΜ”ΎΒψOΘ§«“Γœ1+Γœ3ΘΫ2(Γœ2+Γœ4)Θ§«σœ¬Ν–Ϋ«ΒΡΕ» ΐΘ°(1)Γœ2+Γœ4ΘΜ(2)Γœ1Θ§Γœ2Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com