
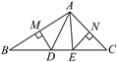
【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.
【答案】(1)BC=10.(2)20°.
【解析】
(1)由AB、AC的垂直平分线分别交BC于D、E,垂足分别是M、N,根据线段垂直平分线的性质,可得AD=BD,AE=EC,继而可得△ADE的周长等于BC的长;
(2)由∠BAC=100゜,可求得∠B+∠C的度数,又由AD=BD,AE=EC,即可求得∠BAD+∠CAE的度数,继而求得答案.
解:(1)因为AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N,
所以AD=BD,AE=CE.
因为△ADE的周长是10,
所以AD+DE+AE=BD+DE+CE=BC=10,即BC=10.
(2)因为∠BAC=100°,
所以∠B+∠C=180°-∠BAC=80°.
因为AD=BD,AE=CE,
所以∠BAD=∠B,∠CAE=∠C,
所以∠BAD+∠CAE=80°,所以∠DAE=∠BAC-(∠BAD+∠CAE)=100°-80°=20°.


科目:初中数学 来源: 题型:
【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
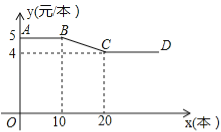
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
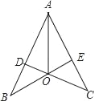
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,如果AB=AC,那么图中全等的三角形有( )
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
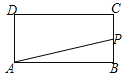
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A. 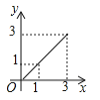 B.
B. 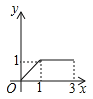 C.
C. 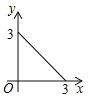 D.
D. 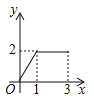
查看答案和解析>>
科目:初中数学 来源: 题型:
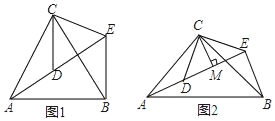
【题目】(1)问题探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
①求证:△CDA≌△CEB;
②求∠AEB的度数.
(2)问题变式:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①请求出∠AEB的度数
②直接写出线段AE、CM、BE之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( ) 
A.2周
B.3周
C.4周
D.5周
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )

A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
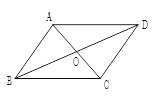
A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
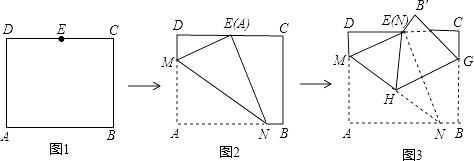
【题目】如图,在矩形ABCD中,AB=8 ![]() ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG= ![]()
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com