
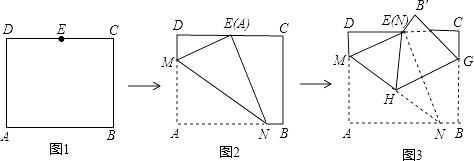
����Ŀ����ͼ���ھ���ABCD�У�AB=8 ![]() ��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG=
��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG= ![]()
A.1��
B.2��
C.3��
D.4��
���𰸡�C
���������⣺��ͼ3�����۵��ɵã���MEN=��A=90�㣬HG��NE�� ��ME��EN��HG��EN��
��EM��GH���ʢ���ȷ��
���NME=��NHG��
���۵��ɵã���NME=��AMN����EHG=��NHG��
���AMN=��EHG���ʢ���ȷ��
��ͼ2����NF��CD��F��
��DM=x����AM=EM=10��x��
�ߵ�E��CD���е㣬AB=CD=8 ![]() ��
��
��DE= ![]() CD=4
CD=4 ![]() ��
��
��Rt��DEM����DM2+DE2=EM2 ��
�ࣨ4 ![]() ��2+x2=��10��x��2 ��
��2+x2=��10��x��2 ��
���x=2.6��
��DM=2.6��AM=EM=7.4��
�ߡ�DEM+��NEF=90�㣬��NEF+��ENF=90�㣬
���DEM=��ENF��
�ߡ�D=��EFN=90�㣬
���DME�ס�FEN��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��EN= ![]() ��
��
��AN= ![]() ��
��
��tan��AMN= ![]() =
= ![]() ��
��
��tan��EHG= ![]() ���ʢ���ȷ��
���ʢ���ȷ��
�֡�tan60��= ![]() ��
�� ![]() ��
��
���AMN��60�㣬����EMH��60�㣬
���MEH���ǵȱ������Σ��ʢڴ���
����ȷ�Ľ�����3����
��ѡ��C��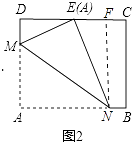
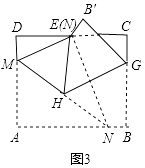
�����㾫����������Ŀ����֪���������þ��ε����ʺͷ��۱任���۵����⣩�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���վ��ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ��۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
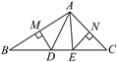
����Ŀ����ͼ����ABC�У�AB��AC�Ĵ�ֱƽ���߷ֱ�BC��D��E���㣬����ֱ���M��N.
(1)����ADE���ܳ���10����BC�ij���
(2)����BAC��100�㣬���DAE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ��귨���������У��ҹ�ѡ�������ھ����гɹ����ܶ��ֶ�ڣ���Ϊ��÷����������ھ�������һ�ˣ�ij������ίԱ�ͱ���ͬѧ�Ըý취�����������˽�̶Ƚ���ȫ�����ͳ�ƣ��ռ����ݺ������������������ͳ��ͼ����ͼ��1����ͼ��2��������ͼ�е���Ϣ������������⣺ 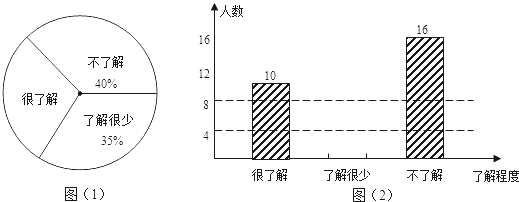
��1���ð����ѧ����
��2����ͼ��1���У������˽⡱����Ӧ��Բ�ĽǵĶ���Ϊ��
��3����ͼ��2���е�����ͼ�β���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC����B=90�㣬AD=6cm��AB=8cm��BC=14cm������P��Q���ӵ�C��������P��C��B�����������˶�����Q��C��D��A�����������˶�����P��Q����һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶��� 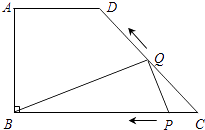
��1����CD�ij���
��2������P��1cm/s�ٶ��˶�����Q��2 ![]() cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3������P���ٶ�����1cm/s����Q���ٶ�Ϊacm/s��Ҫʹ���˶������г���PQ��DC������ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ��l1��l2�ཻ�ڵ�O���ҡ�1+��3��2(��2+��4)�������нǵĶ�����(1)��2+��4��(2)��1����2��
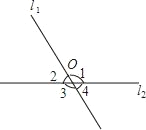
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
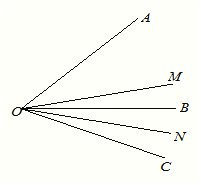
����Ŀ����ͼ��ʾ��֪![]() ��
��![]() ��OMƽ��
��OMƽ��![]() ��ONƽ��
��ONƽ��![]() ��
��
(1)![]() ��
��
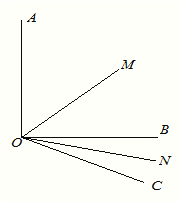
(2)��ͼ��AOB��900����OC��O��������ת��ʹ��BOC��![]() ����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ������ֵ�������ܣ���˵�����ɣ�
����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ������ֵ�������ܣ���˵�����ɣ�

(3)![]() ��
��![]() ����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ���
����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ���![]() �Ķ����������������п���ʲôʲô������
�Ķ����������������п���ʲôʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���ͼ�ش����⣺ 
��1��ָ��С������ҵ����һ����ʼ���ֵĴ�����������������������ȷ�����
��2����a��b�Dz���ʽ�� ![]() �������⣨a��b����������{}��ʽ��ֵ��
�������⣨a��b����������{}��ʽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ĸ�������AB=DE��BC=EF����B=��E����C=��F��������ѡ����������ʹ��ABC����DEF�Ĺ��У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���С��ͬ��С�������һ�������壬ʹ�ô�����ʹ����濴����������������״��ͼ��ʾ
��1���뻭��һ�ִ����濴����������״ͼ��
��2���������������Ĵ����濴������״ͼ����ϴ�����ʹ����濴����������������״ͼֱ��д���������������Ҫ��С������ĸ�����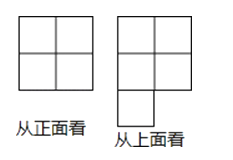
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com