
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC����B=90�㣬AD=6cm��AB=8cm��BC=14cm������P��Q���ӵ�C��������P��C��B�����������˶�����Q��C��D��A�����������˶�����P��Q����һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶��� 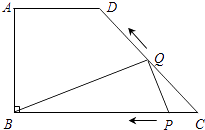
��1����CD�ij���
��2������P��1cm/s�ٶ��˶�����Q��2 ![]() cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3������P���ٶ�����1cm/s����Q���ٶ�Ϊacm/s��Ҫʹ���˶������г���PQ��DC������ֱ��д��a��ȡֵ��Χ��
���𰸡�
��1���⣺��D����DH��BC������Ϊ��H��
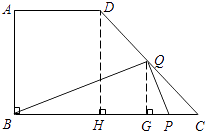
����DH=AB=8cm��BH=AD=6cm��
��CH=BC��BH=14��6=8cm��
��Rt��DCH�У���DHC=90�㣬
��CD= ![]() =8
=8 ![]() cm��
cm��
��2���⣺����P��Q�˶���ʱ��Ϊt��s������PC=t��
�� ����Q��CD��ʱ����Q����QG��BC������Ϊ��G����QC=2 ![]() t��
t��
�֡�DH=HC��DH��BC��
���C=45�㣮
����Rt��QCG��QG=QCsin��C=2 ![]() t��sin45��=2t��
t��sin45��=2t��
�֡�BP=BC��PC=14��t��
��S��BPQ= ![]() BP��QG=
BP��QG= ![]() ��14��t����2t=14t��t2��
��14��t����2t=14t��t2��
��Q�˶���D��ʱ����Ҫ��ʱ��t= ![]() =
= ![]() =4��
=4��
��S=14t��t2��0��t��4����
�ڵ���Q��DA��ʱ����Q����QG��BC������Ϊ��G��
��QG=AB=8cm��BP=BC��PC=14��t��
��S��BPQ= ![]() BP��QG=
BP��QG= ![]() ��14��t����8=56��4t��
��14��t����8=56��4t��
��Q�˶���A��ʱ����Ҫ��ʱ��t= ![]() =
= ![]() =4+
=4+ ![]() ��
��
��S=56��4t��4��t��4+ ![]() ����
����
�ۺ�����������ĺ�����ϵʽ�ǣ�
S=14t��t2��0��t��4����
S=56��4t��4��t��4+ ![]() ����
����
��3���⣺Ҫʹ�˶������г���PQ��DC��
��AD��BC����CPQD��ƽ���ı��Σ�
��CP=DQ��
1t=at��8 ![]() ��
��
��t= ![]() �٣�
�٣�
�֡�Q����AD���ϣ�
�� ![]() ��t��
��t�� ![]() �ڣ�
�ڣ�
�Ѣٴ���ڣ����a��1+ ![]() ��
��
��a��ȡֵ��Χ��a��1+ ![]() ��
��
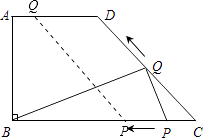
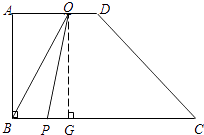
����������1����D����DH��BC������Ϊ��H������Rt��DCH�У���DH��CH�ij��ȣ����ù��ɶ����������CD�ij�����2�����ڵ�P���߶�CB���˶�������Q��C��D��A�����������˶������Է�����������ۣ��ٵ�Q��CD�ϣ��ڵ�Q��DA�ϣ����ÿһ������������Թ�Q����QG��BC��G�����ڵ�P��Q�˶���ʱ��Ϊt��s�������ú�t�Ĵ���ʽ�ֱ��ʾBP��QG�ij��ȣ�Ȼ����������ε������ʽ�������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ����3����DQ=CP��Q����AD���ϣ����a��ȡֵ��Χ��
�����㾫����������Ҫ�����˹��ɶ����ĸ����ֱ�����ε����֪ʶ�㣬��Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��һ����ֱ�ڵ�������ֱ�����β�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
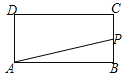
����Ŀ����ͼ���ڳ�����ABCD�У�AB��2��BC��1���˵�P�ӵ�B��������·��B![]() C
C![]() D�������˶�����ô��ABP�����
D�������˶�����ô��ABP�����![]() ���P�˶���·��֮��ĺ���ͼ������ǣ� ��.
���P�˶���·��֮��ĺ���ͼ������ǣ� ��.
A. 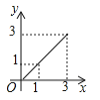 B.
B. 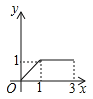 C.
C. 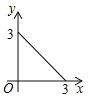 D.
D. 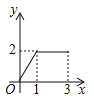
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж��ı���ABCDΪƽ���ı��ε���( )
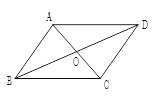
A. AB��CD��AD��BC B. OA=OC��OB=OD C. AD=BC��AB��CD D. AB=CD��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չУ�����˶������س�����У�������Ϲ���һ�������˶�װ�����г����鷢�֣��ס������̳���ͬ���ļ۸����ͬ��Ʒ�Ƶ�����ӷ���������֪ÿ�ӷ���ÿ�������50Ԫ�����ӷ�����������ķ�����ȣ���Ǣ̸�����̳��Żݷ����ǣ�ÿ����ʮ�ӷ�����һ���������̳��Żݷ����ǣ�������ӷ�����80�ף�����ӷ������ۣ������������ۣ�
��1����ÿ�ӷ���ÿ������ļ۸��Ƕ��٣�
��2����������У���Ϲ���100�ӷ���a������aΪ����ʱ���������̳�����һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��![]() ��2����
��2����![]() -
-![]() ������-
������-![]() ��
��
��3��![]() ��4����-2a2��3+ a8��a2 +3a��a5
��4����-2a2��3+ a8��a2 +3a��a5
��5��(2x-5)(2x+5)-2x(2x-3) ��6��(3x+y)2-(3x-y)2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������λ�ڵ�A���һ�㣬��AB=20������P�ӵ�A��������3����λ/����ٶ��������Ḻ���������˶������˶�ʱ��Ϊt�루t��0����
![]()
��1��д�������ϵ�B��ʾ���� ������P��Ӧ������ ���ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������1����λ/����ٶ������˶����ҵ�P, Qͬʱ����
��������Q�������������������˶���������ʱ��P���Q������
��������Q�������Ḻ���������˶���������ʱ��P���Q���4����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
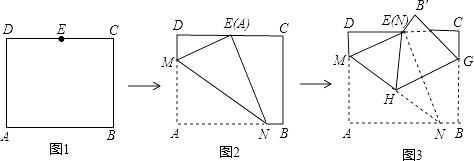
����Ŀ����ͼ���ھ���ABCD�У�AB=8 ![]() ��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG=
��AD=10����E��CD���е㣬������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غϣ���ͼ2���ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غϣ���ͼ3����B�䵽B�䴦���ۺ�ΪHG������HE�������н�����ȷ�ĸ����ǣ� �� ��ME��HG���ڡ�MEH�ǵȱ������Σ��ۡ�EHG=��AMN����tan��EHG= ![]()
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��130������COD��80����OM��ON�ֱ��ǡ�AOB�͡�COD��ƽ���ߣ�
(1)���OA��OC�غϣ���OD�ڡ�AOB���ڲ�����ͼ1�����MON�Ķ�����
(2)�����ͼ1�еġ�COD�Ƶ�O��˳ʱ����תn��(0��n��155)����ͼ2��
�١�MON����ת����n����������������ϵ��˵�����ɣ�
�ڵ�nΪ����ʱ����MONΪֱ�ǣ�
(3)�����AOB��λ�úʹ�С���䣬��COD�ı�OD��λ�ò��䣬�ı��COD�Ĵ�С����ͼ1�е�OC����O��˳ʱ����תm��(0��m��100)����ͼ3����MON����ת����m����������������ϵ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1������ͬѧ���ֹ�ֽ����һ��̨�Ƶ��֣��뻭����������������ͼ����ͼ��
��2����ͼ2����ֱ֪��AB��CD�ཻ�ڵ�O��EO��AB��OF�ǡ�AOC��ƽ���ߣ���EOC=![]() ��AOC�����DOF�Ķ�����
��AOC�����DOF�Ķ�����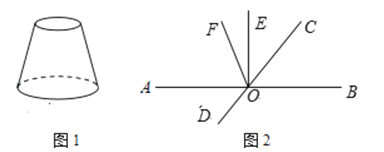
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com