
【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

【答案】(1)25°;(2)①n°+25°,②n=65°;(3)![]() m°+25°.
m°+25°.
【解析】
(1)如图1,根据OM平分∠AOB,∠AOB=130°,利用角平分线的定义可得:∠AOM=![]() ∠AOB=
∠AOB=![]() ×130°=65°,再根据ON平分∠COD,∠COD=80°,可得∠AON=
×130°=65°,再根据ON平分∠COD,∠COD=80°,可得∠AON=![]() ∠COD=
∠COD=![]() ×80°=40°,
×80°=40°,
进而求出∠MON=∠AOM﹣∠AON=65°﹣40°=25°,
(2)①如图2中,根据图形中角的和差关系可得:∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,
②当∠MON=90°时,由于n°+25°=90°,所以n=65°,
(3)如图3中,根据图中角的和差关系可得:∠MON=∠COM﹣∠CON=65°+m°﹣![]() (80°+m°)=
(80°+m°)=![]() m°+25°.
m°+25°.
(1)如图1,∵OM平分∠AOB,∠AOB=130°,
∴∠AOM=![]() ∠AOB=
∠AOB=![]() ×130°=65°,
×130°=65°,
∵ON平分∠COD,∠COD=80°,
∴∠AON=![]() ∠COD=
∠COD=![]() ×80°=40°,
×80°=40°,
∴∠MON=∠AOM﹣∠AON=65°﹣40°=25°,
(2)①如图2中,∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,
②当∠MON=90°时,n°+25°=90°,
∴n=65°,
(3)如图3中,∠MON=∠COM﹣∠CON=65°+m°﹣![]() (80°+m°)=
(80°+m°)=![]() m°+25°.
m°+25°.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点. 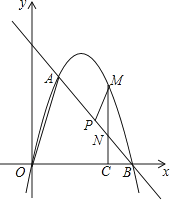
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,从节省资金的角度考虑,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.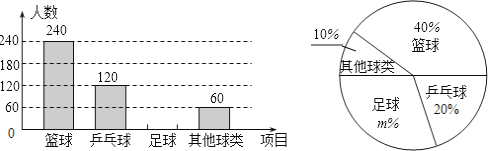
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有△人;在扇形图中,m=△;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )

A. (﹣1,![]() ) B. (﹣2,
) B. (﹣2,![]() ) C. (﹣
) C. (﹣![]() ,1) D. (﹣
,1) D. (﹣![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( ) 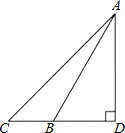
A.2 ![]() m
m
B.2 ![]() m
m
C.(2 ![]() ﹣2)m
﹣2)m
D.(2 ![]() ﹣2)m
﹣2)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:(a×b)2=a2×b2、(a×b)3=a3×b3、(a×b)4=a4×b4,
(1)用具体数值验证上述等式是否成立(写出其中一个验证过程)
(2)通过上述验证,猜一猜:(a×b)100= ,归纳得出:(a×b)n= ;
(3)请应用上述性质计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 ![]() cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com