
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )

A. (﹣1,![]() ) B. (﹣2,
) B. (﹣2,![]() ) C. (﹣
) C. (﹣![]() ,1) D. (﹣
,1) D. (﹣![]() ,2)
,2)
【答案】A
【解析】
过点C作CE⊥x轴于点E,在RT△AOB中,求出AO的长,根据旋转的性质可得AO=CD=4、OB=BD、△OBD是等边三角形,进而可得RT△COE中∠COE=60°、CO=2,由三角函数可得OE、CE.
过点C作CE⊥x轴于点E,

∵OB=2,AB⊥x轴,点A在直线y=![]() x上,
x上,
∴AB=2![]() ,OA=
,OA=![]() =4,
=4,
∴RT△ABO中,tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
又∵△CBD是由△ABO绕点B逆时针旋转60°得到,
∴∠D=∠AOB=∠OBD=60°,AO=CD=4,
∴△OBD是等边三角形,
∴DO=OB=2,∠DOB=∠COE=60°,
∴CO=CDDO=2,
在RT△COE中,OE=COcos∠COE=2×![]() =1,
=1,
CE=COsin∠COE=2×![]() =
=![]() ,
,
∴点C的坐标为(1,![]() ),
),
故选:A.


科目:初中数学 来源: 题型:
【题目】小明自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装.为了缓解资金压力,小明决定打折销售.若每件服装按标价的![]() 折出售将亏
折出售将亏![]() 元,而按标价的
元,而按标价的![]() 折出售将赚
折出售将赚![]() 元.
元.
(1)请你算一算每件服装的标价是多少元?
(2)为了尽快减少库存,又要保证不亏本,请你告诉小明最多能打几折.
(3)小明认真总结了前一次的教训,进行了详细的市场调查后第二次进货![]() 件,按第一次的标价销售了
件,按第一次的标价销售了![]() 件后,剩下的进行打折甩卖,为了尽快减少库存,又要保证盈利两万元钱,请你告诉小明最多能打几折.
件后,剩下的进行打折甩卖,为了尽快减少库存,又要保证盈利两万元钱,请你告诉小明最多能打几折.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.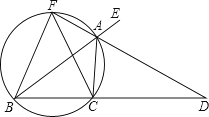
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张直角三角形纸片ABC,边![]() ,
,![]() ,
,![]() ,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为
,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为![]()
![]()

A. 16 B. 17 C. 18 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 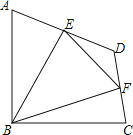
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB= ![]() ,E是
,E是 ![]() 的中点,求EGED的值.
的中点,求EGED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如![]() 不能表示为两个互质的整数的商,所以
不能表示为两个互质的整数的商,所以![]() 几个号无理数.可以这样证明:
几个号无理数.可以这样证明:
设![]() ,a与b是互质的两个整数,且b≠0,则2=
,a与b是互质的两个整数,且b≠0,则2=![]() ,所以a=2b.
,所以a=2b.
因为b是整数且不为0,所以a是不为0的偶数.设a=2n(n是整数),
所以b=2n,所以b也是偶数,与a与b是互质的整数矛盾,
所以![]() 是无理数.
是无理数.
仔细阅读上文,然后请证明:![]() 是无理数。
是无理数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com