
����Ŀ��С��������ҵ����һ�ҷ�װ�꣬��Ϊ����ʱû�н����г����飬�ڻ���ʱ��ѹ��һ����װ��Ϊ�˻����ʽ�ѹ����С�������������ۣ���ÿ����װ����۵�![]() �۳��۽���
�۳��۽���![]() Ԫ��������۵�
Ԫ��������۵�![]() �۳��۽�
�۳��۽�![]() Ԫ��
Ԫ��
��1��������һ��ÿ����װ�ı���Ƕ���Ԫ��
��2��Ϊ�˾�����ٿ�棬��Ҫ��֤���������������С������ܴ��ۣ�
��3��С�������ܽ���ǰһ�εĽ�ѵ����������ϸ���г������ڶ��ν���![]() ��������һ�εı��������
��������һ�εı��������![]() ����ʣ�µĽ��д���˦����Ϊ�˾�����ٿ�棬��Ҫ��֤ӯ������ԪǮ���������С������ܴ��ۣ�
����ʣ�µĽ��д���˦����Ϊ�˾�����ٿ�棬��Ҫ��֤ӯ������ԪǮ���������С������ܴ��ۣ�
���𰸡���1��ÿ����װ�ı����![]() Ԫ����2������ܴ�
Ԫ����2������ܴ�![]() �ۣ���3��С������ܴ�
�ۣ���3��С������ܴ�![]() �ۣ�
�ۣ�
��������
��1��������ÿ����װ�ı����xԪ������ÿ����װ�ijɱ������Լ�����ÿ����װ����۵�5�۳��۽���20Ԫ��������۵�8�۳��۽�40Ԫ���������г����̣�
��2��Ϊ�˾�����ٿ�棬��Ҫ��֤��������Ҳ���Ǵ��ۺ��ۼ۵��ڳɱ����ڣ�1���Ľ��۵Ļ����ϣ��з��̽�ɣ�
��3�����ݣ�1������ı�ۣ�����ó��ɱ���Ȼ����С������ܴ�x�ۣ��ҳ�������ϵ����ӯ������Ԫ���г����̣���⼴�ɣ�
��1����ÿ����װ�ı����![]() Ԫ��
Ԫ��
������ã�![]() ��
��
��ã�![]() ��
��
��ÿ����װ�ı����![]() Ԫ��
Ԫ��
��2��������![]() �ۣ�
�ۣ�
������ã�![]() ��
��
��ã�![]() ��
��
������ܴ�![]() �ۣ�
�ۣ�
��3���ɣ�1���ã��ɱ�Ϊ��![]() ��Ԫ����
��Ԫ����
��С������ܴ�![]() �ۣ�
�ۣ�
������ã�![]() ��
��
��ã�![]() ��
��
��С������ܴ�![]() �ۣ�
�ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��x��0����ͼ����A��2����1����B��
��x��0����ͼ����A��2����1����B�� ![]() ��n�����㣬ֱ��y=2��y�ύ�ڵ�C��
��n�����㣬ֱ��y=2��y�ύ�ڵ�C�� 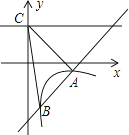
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2��bx��2��a��0����ͼ��Ķ����ڵ������ޣ��ҹ��㣨��1��0������a��bΪ����ʱ��ab��ֵΪ��������
A.![]() ��1
��1
B.![]() ��1
��1
C.![]() ��
�� ![]()
D.![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=��![]() x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B����ABΪ���ڵ�һ���������ȱ���ABC
x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B����ABΪ���ڵ�һ���������ȱ���ABC

��1������ABC������͵�C�����ꣻ
��2������ڵڶ���������һ��P��a��![]() �������ú�a�Ĵ���ʽ��ʾ�ı���ABPO�������
�������ú�a�Ĵ���ʽ��ʾ�ı���ABPO�������
��3����x�����Ƿ���ڵ�M��ʹ��MABΪ���������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������y=mx2+nx�ཻ��A��1��3 ![]() ����B��4��0�����㣮
����B��4��0�����㣮 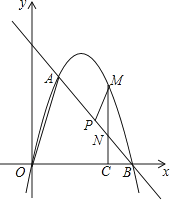
��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN �� ��� ![]() ��ֵ���������ʱ��M�����꣮
��ֵ���������ʱ��M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�
��1��2��x��1��+1=0
��2��4��2x��1����3��5x+1��=14
��3��x��![]() =1��
=1��![]()
��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤��

��1����AEF�ա�CEB��
��2��AF=2CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֻ�׳���5��5�ķ���ÿС��߳�Ϊ1���������������˶�.����A������ȥ����B��C��D���������׳棬�涨������������Ϊ��������������Ϊ��.�����A��B��Ϊ��A��B(+1��+4)����B��A��Ϊ��B��A(-1��-4)�����е�һ������ʾ���ҷ��ڶ�������ʾ���·���
��1��ͼ��A��C( �� )��B��C( �� )��C�� (+1�� )��
��2������ֻ�׳��A��ȥ�׳�P��������·������Ϊ��+2��+2������+2��-1������-2��+3������-1��-2��������ͼ�б��P��λ�ã�

��3������ֻ�׳������·��ΪA��B��C��D�������ü׳��߹���·�̣�
��4����ͼ�������������M��N����M��A��3-a��b-4����M��N��5-a��b-2������N��AӦ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=![]() x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60���õ���CBD������B������Ϊ��2��0�������C������Ϊ��������
x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60���õ���CBD������B������Ϊ��2��0�������C������Ϊ��������

A. ����1��![]() �� B. ����2��
�� B. ����2��![]() �� C. ����
�� C. ����![]() ��1�� D. ����
��1�� D. ����![]() ��2��
��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com