
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,从节省资金的角度考虑,应该选择哪个工程队?
【答案】解:设甲队单独完成此项工程需要x天,乙队单独完成需要(x+5)天.
依据题意可列方程: ![]() +
+ ![]() =
= ![]() ,
,
解得:x1=10,x2=﹣3(舍去).
经检验:x=10是原方程的解.
设甲队每天的工程费为y元.
依据题意可列方程:6y+6(y﹣4000)=385200,
解得:y=34100.
甲队完成此项工程费用为34100×10=341000元.
乙队完成此项工程费用为30100×15=451500元.
答:从节省资金的角度考虑,应该选择甲工程队
【解析】设甲队单独完成此项工程需要x天,乙队单独完成需要(x+5)天,然后依据6天可以完成,列出关于x的方程,从而可求得甲、乙两队单独完成需要的天数,然后设甲队每天的工程费为y元,则可表示出乙队每天的工程费,接下来,根据两队合作6天的工程费用为385200元列方程求解,于是可得到两队独做一天各自的工程费,然后可求得完成此项工程的工程费,从而可得出问题的答案.本题主要考查的是分式方程的应用、一元一次方程的应用,根据题意列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:
【题目】体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x, y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )

A. y=x+9与![]() B. y=-x+9与
B. y=-x+9与![]()
C. y=-x+9与![]() D. y=x+9与
D. y=x+9与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由若干个棱长为1cm的完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;

(2)在露出的表面上涂上颜色(不含底面),则涂上颜色部分的总面积为 cm2.
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的三视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.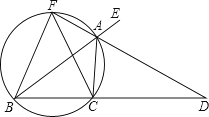
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )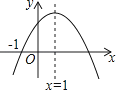
A.a>0
B.c<0
C.3是方程ax2+bx+c=0的一个根
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com