
【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
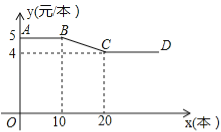
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
【答案】(1)购买不超过10本此种笔记本时售价为5元/本.(2)①当0<x≤10时,y=5;②当10<x≤20时,y=﹣0.1x+6;③当20<x时,y=4.(3)当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.
【解析】
试题(1)观察一次函数图象可知线段AB与x轴平行,即可得出线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本;(2)观察一次函数图象可知,图象分三段,因此y与x之间的函数关系式分三种情况,①当0<x≤10时,②当10<x≤20时,③当x>20时,根据这三种情况分别求出y与x之间的函数关系式即可;(3)根据题意求出W与x之间的关系式,再利用二次函数的性质即可求解.
试题解析: 解:(1)图中线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本.
(2)①当0<x≤10时,
y与x之间的函数关系式y=5,
②当10<x≤20时,
设=kx+b把B(10,5),C(20,4)代入得![]() ,
,
解得![]() .
.
所以y与x之间的函数关系式y=﹣0.1x+6.
③当x>20时,y与x之间的函数关系式为:y=4.
(3)W=(﹣0.1x+6﹣3)x=﹣0.1×(x﹣15)2+22.5.
答:当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:![]() =1÷4=0.25;
=1÷4=0.25;![]() =
=![]() =8÷5=1.6;
=8÷5=1.6;![]() =1÷3=
=1÷3=![]() ,反之,0.25=
,反之,0.25=![]() =
=![]() ;1.6=
;1.6=![]() =
=![]() =
=![]() .那么
.那么![]() ,
,![]() 怎么化成分数呢?
怎么化成分数呢?
解:∵![]() ×10=3+
×10=3+![]() , ∴不妨设
, ∴不妨设![]() =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x=![]() ,即
,即![]() =
=![]() ;
;
∵![]() =
=![]() ,设
,设![]() =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=![]() ,
,
∴![]() =
=![]() =1+x=1+
=1+x=1+![]() =
=![]()
⑴将分数化为小数:![]() =______,
=______,![]() =_______;
=_______;
⑵将小数化为分数:![]() =______,
=______,![]() =_______;
=_______;
⑶将小数![]() 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司决定利用仅有的349个甲种部件和295个乙种部件组装A、B两种型号的简易板房共50套捐赠给灾区.已知组装一套A型号简易板房需要甲种部件8个和乙种部件4个,组装一套B型号简易板房需要甲种部件5个和乙种部件9个.
(1)该公司组装A、B两种型号的简易板房时,共有多少种组装方案?
(2)若组装A、B两种型号的简易板房所需费用分别为每套200元和180元,问最少总组装费用是多少元?并写出总组装费用最少时的组装方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇左市江州区太平镇壶城社区调查居民双休日的学习状况,采取了下列调查方式;a:从崇左高中、太平镇中、太平小学三所学校中选取200名教师;b:从不同住宅楼(即江湾花园与万鹏住宅楼)中随机选取200名居民;c:选取所管辖区内学校的200名在校学生.并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图.以下结论:①上述调查方式最合理的是b;②在这次调查的200名教师中,在家学习的有60人;③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人;④小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是0.1.其中正确的结论是( ) 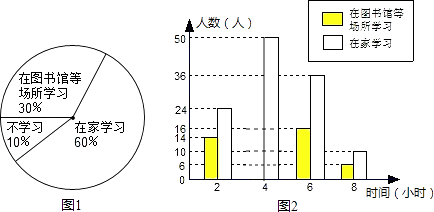
A.①④
B.②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)的顶点坐标为点A(﹣2,3),且抛物线y=ax2+bx+c与y轴交于点B(0,2).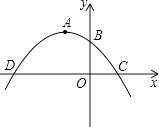
(1)求该抛物线的解析式;
(2)是否在x轴上存在点P使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P是x轴上任意一点,则当PA﹣PB最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
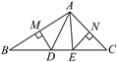
【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com