
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)的顶点坐标为点A(﹣2,3),且抛物线y=ax2+bx+c与y轴交于点B(0,2).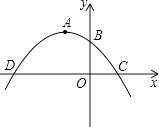
(1)求该抛物线的解析式;
(2)是否在x轴上存在点P使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P是x轴上任意一点,则当PA﹣PB最大时,求点P的坐标.
【答案】
(1)
解:∵抛物线的顶点坐标为A(﹣2,3),∴可设抛物线的解析式为y=a(x+2)2+3.
由题意得:a(0+2)2+3=2,解得:a=﹣ ![]() .
.
∴物线的解析式为y=﹣ ![]() (x+2)2+3,即y=﹣
(x+2)2+3,即y=﹣ ![]() x2﹣x+2.
x2﹣x+2.
(2)
解:设存在符合条件的点P,其坐标为(p,0),则
PA2=(﹣2﹣p)2+32,PB2=p2+22,AB2=(3﹣2)2+22=5
当PA=PB时,(﹣2﹣p)2+32=p2+22,解得:p=﹣ ![]() ;
;
当PA=AB时,(﹣2﹣p)2+32=5,方程无实数解;
当PB=AB时,p2+22=5,解得p=±1.
∴x轴上存在符合条件的点P,其坐标为(﹣ ![]() ,0)或(﹣1,0)或(1,0).
,0)或(﹣1,0)或(1,0).
(3)
解:∵PA﹣PB≤AB,
∴当A、B、P三点共线时,可得PA﹣PB的最大值,这个最大值等于AB,此时点P是直线AB与x轴的交点.
设直线AB的解析式为y=kx+b,则:
![]() ,解得
,解得 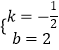 .
.
∴直线AB的解析式为y=﹣ ![]() x+2,
x+2,
当y=﹣ ![]() x+2=0时,解得x=4.
x+2=0时,解得x=4.
∴当PA﹣PB最大时,点P的坐标是(4,0).
【解析】(1)通过读题可以看出抛物线y=ax2+bx+c(a≠0)的顶点坐标为点A(﹣2,3),且经过B点,所以直接将抛物线的解析式设为顶点式,然后代入B点的坐标求解即可.(2)首先设出P点的坐标,根据坐标系两点间的距离公式分别求出PA、PB、AB的长度(或表达式),然后分PA=PB、PA=AB、PB=AB三种情况列方程求解即可.(3)当P、A、B三点不共线时,PA﹣PB<AB(三角形三边关系定理),三点共线时,PA﹣PB=AB,综合来看:PA﹣PB≤AB,所以当PA﹣PB的值最大时,P、A、B三点共线,因此只需求出直线AB的解析式,该直线与x轴的交点即为符合条件的P点.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )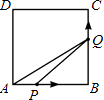
A.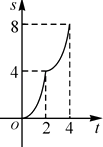
B.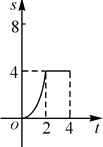
C.
D.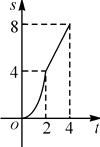
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.

(1)根据图象求出b关于a的函数解析式(包括自变量的取值范围);
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m千米,设农场从A公司购买x吨铵肥,购买8吨铵肥的总费用为y元(总费用=购买铵肥费用+运输费用),求出y关于x的函数解析式(m为常数),并向农场建议总费用最低的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
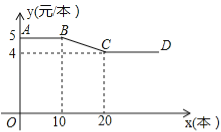
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C. 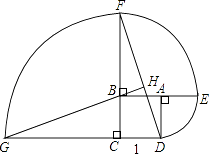
(1)求点D沿三条弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则PEF和PGH的面积和等于.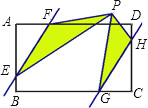
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,如果AB=AC,那么图中全等的三角形有( )
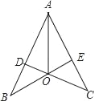
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )

A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com