
【题目】如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C. 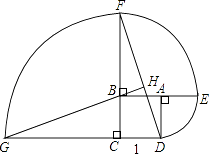
(1)求点D沿三条弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
【答案】
(1)解:根据弧长公式得所求路线长为:
![]() =3π.
=3π.
(2)解:GB⊥DF.
理由如下:
在△FCD和△GCB中,
∵ 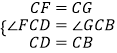 ,
,
∴△FCD≌△GCB(SAS),
∴∠G=∠F,
∵∠F+∠FDC=90°,
∴∠G+∠FDC=90°,
∴∠GHD=90°,
∴GB⊥DF.
【解析】(1)根据弧长的计算公式,代入运算即可.(2)先证明△FCD≌△GCB,得出∠G=∠F,从而利用等量代换可得出∠GHD=90°,即GB⊥DF.
【考点精析】本题主要考查了正方形的性质和弧长计算公式的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇左市江州区太平镇壶城社区调查居民双休日的学习状况,采取了下列调查方式;a:从崇左高中、太平镇中、太平小学三所学校中选取200名教师;b:从不同住宅楼(即江湾花园与万鹏住宅楼)中随机选取200名居民;c:选取所管辖区内学校的200名在校学生.并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图.以下结论:①上述调查方式最合理的是b;②在这次调查的200名教师中,在家学习的有60人;③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人;④小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是0.1.其中正确的结论是( ) 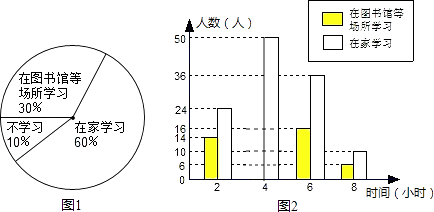
A.①④
B.②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P. 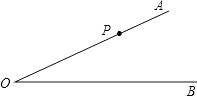
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)的顶点坐标为点A(﹣2,3),且抛物线y=ax2+bx+c与y轴交于点B(0,2).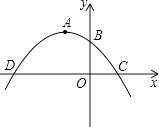
(1)求该抛物线的解析式;
(2)是否在x轴上存在点P使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P是x轴上任意一点,则当PA﹣PB最大时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com