
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,如果AB=AC,那么图中全等的三角形有( )
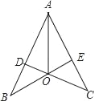
A. 2对 B. 3对 C. 4对 D. 5对
【答案】C
【解析】
共有四对.分别为△ADO≌△AEO,△ADC≌△AEB,△ABO≌△ACO,△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.
:
 ∵CD⊥AB,BE⊥AC,AO平分∠BAC
∵CD⊥AB,BE⊥AC,AO平分∠BAC
∴∠ADO=∠AEO=90![]() ,∠DAO=∠EAO,
,∠DAO=∠EAO,
∵在△ADO和△AEO中
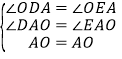 ,
,
∴△ADO≌△AEO(AAS);
∴OD=OE,AD=AE
∵在△BOD和△COE中
 ,∴△BOD≌△COE(ASA);
,∴△BOD≌△COE(ASA);
∴BD=CE,OB=OC,∠B=∠C,
在△ADC和△AEB中
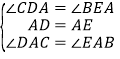 ,
,
∴△ADC≌△AEB(ASA);
在△ABO和△ACO中
 ,
,
∴△ABO≌△ACO(SSS).
所以共有四对全等三角形。
故答案选:C.


科目:初中数学 来源: 题型:
【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:![]() =1÷4=0.25;
=1÷4=0.25;![]() =
=![]() =8÷5=1.6;
=8÷5=1.6;![]() =1÷3=
=1÷3=![]() ,反之,0.25=
,反之,0.25=![]() =
=![]() ;1.6=
;1.6=![]() =
=![]() =
=![]() .那么
.那么![]() ,
,![]() 怎么化成分数呢?
怎么化成分数呢?
解:∵![]() ×10=3+
×10=3+![]() , ∴不妨设
, ∴不妨设![]() =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x=![]() ,即
,即![]() =
=![]() ;
;
∵![]() =
=![]() ,设
,设![]() =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=![]() ,
,
∴![]() =
=![]() =1+x=1+
=1+x=1+![]() =
=![]()
⑴将分数化为小数:![]() =______,
=______,![]() =_______;
=_______;
⑵将小数化为分数:![]() =______,
=______,![]() =_______;
=_______;
⑶将小数![]() 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)的顶点坐标为点A(﹣2,3),且抛物线y=ax2+bx+c与y轴交于点B(0,2).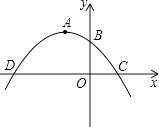
(1)求该抛物线的解析式;
(2)是否在x轴上存在点P使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P是x轴上任意一点,则当PA﹣PB最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AB上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E.(要求:尺规作图,保留作图痕迹,但不必写出作法);
(2)在(1)的条件下,求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在横线上填写合适的内容,完成下面的证明:
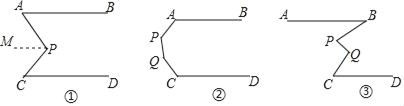
(1)如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB,
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以PM∥CD( )
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C( )
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
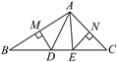
【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年法国网球公开赛中,我国选手李娜在决赛中成功击败对手夺冠,称为获得法国网球公开赛冠军的亚洲第一人.某班体育委员就本班同学对该届法国网球公开赛的了解程度进行全面调查统计,收集数据后绘制了两幅不完整的统计图,如图(1)和图(2).根据图中的信息,解答下列问题: 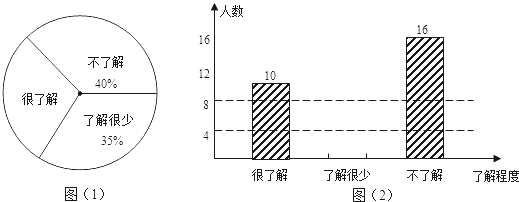
(1)该班共有名学生;
(2)在图(1)中,“很了解”所对应的圆心角的度数为;
(3)把图(2)中的条形图形补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com