
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).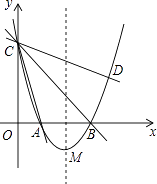
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.
【答案】
(1)
解:将M(2,﹣1)、B(3,0)代入抛物线的解析式中,得:
![]() ,
,
解得 ![]() .
.
故抛物线的解析式:y=x2﹣4x+3.
(2)
解:由抛物线的解析式知:B(3,0)、C(0,3)、A(1,0);
则△OBC是等腰直角三角形,∠OBC=45°.
过B作BE⊥x轴,交直线CD于E(如下图),
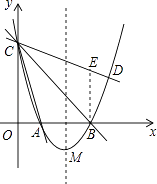
则∠EBC=∠ABC=45°;
由于直线CD和直线CA关于直线CB对称,所以点A、E关于直线BC对称,则BE=AB=2;
则E(3,2).
由于直线CD经过点C(0,3),可设该直线的解析式为y=kx+3,代入E(3,2)后,得:
3k+3=2,k=﹣ ![]()
故直线CD的解析式:y=﹣ ![]() x+3.
x+3.
(3)
解:设P(2,m),已知M(2,﹣1)、B(3,0)、C(0,3),则:
PM2=(2﹣2)2+(m+1)2=m2+2m+1,PB2=(3﹣2)2+(0﹣m)2=m2+1,PC2=(0﹣2)2+(3﹣m)2=m2﹣6m+13;
已知:PM2+PB2+PC2=35,则:m2+2m+1+m2+1+m2﹣6m+13=35,化简得:3m2﹣4m﹣20=0
解之得:m1=﹣2,m2= ![]() ;
;
则P1(2,﹣2)、P2(2, ![]() )
)
当点P坐标为(2, ![]() )时,由图可知,直线OP与抛物线必有两个交点;
)时,由图可知,直线OP与抛物线必有两个交点;
当点P坐标为(2,﹣2)时,直线OP:y=﹣x,联立抛物线的解析式有:
x2﹣4x+3=﹣x,即 x2﹣3x+3=0
△=(﹣3)2﹣4×3<0,
故该直线与抛物线没有交点;
综上,直线OP与抛物线有两个交点.
【解析】(1)抛物线的解析式中只有两个待定系数,将已知的两点坐标代入其中进行求解即可.(2)由C、B两点的坐标不难判断出OB=OC,即∠CBO=45°,那么若取BE⊥x轴交CD于E,结合“直线CD和直线CA关于直线CB对称”可得出A、E关于直线BC对称,结合点B的坐标以及AB的长即可得到点E的坐标,在明确C、E两点坐标的情况下,直线CD的解析式即可由待定系数法求得.(3)先设出点P的坐标,而M、B、C三点坐标已知,即可得到PM2、PB2、PC2的表达式,结合题干的已知条件即可求出点P的坐标,从而进一步判断出直线OP与抛物线的交点个数.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:4,则 ![]() 的值为( )
的值为( ) 
A.2
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 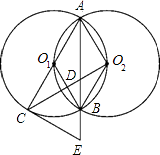
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表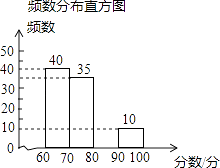
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇左市江州区太平镇壶城社区调查居民双休日的学习状况,采取了下列调查方式;a:从崇左高中、太平镇中、太平小学三所学校中选取200名教师;b:从不同住宅楼(即江湾花园与万鹏住宅楼)中随机选取200名居民;c:选取所管辖区内学校的200名在校学生.并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图.以下结论:①上述调查方式最合理的是b;②在这次调查的200名教师中,在家学习的有60人;③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人;④小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是0.1.其中正确的结论是( ) 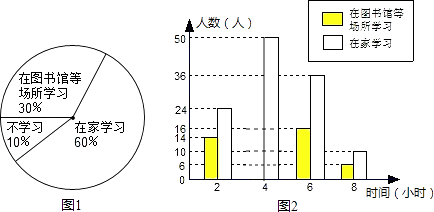
A.①④
B.②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P. 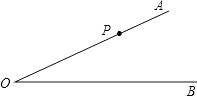
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com