
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示: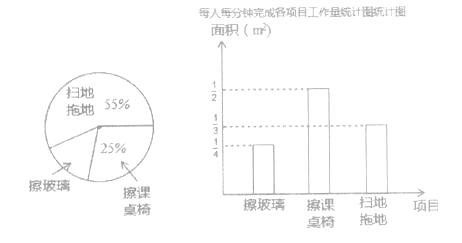
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅
m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
【答案】
(1)20%;![]()
(2)33
(3)
解:设擦玻璃x人,则擦课桌椅(13-x)人,根据题意得:
( ![]() x):[
x):[ ![]() (13-x)]=20:25,
(13-x)]=20:25,
解得:x=8,
经检验x=8是原方程的解.
答:擦玻璃8人,擦课桌椅5人.
【解析】(1)根据题意得:
擦玻璃的面积占总面积的百分比是:1-55%-25%=20%;
每人每分钟擦课桌椅 ![]() m2;
m2;
故答案为:20%, ![]() ;
;
2)扫地拖地的面积是60×55%=33(m2);
故答案为:33.
(1)所有百分比的和为1;观察条形统计图可知;(2)总面积×所占百分比=扫地拖地面积;(3)使“擦玻璃”和“擦课桌椅”同时完成,则擦玻璃的人数×速度×时间:擦课桌椅的人数×速度×时间=20:25.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某玩具厂分别安排甲乙两个车间加工1000个同一型号的奥运会吉祥物,每名工人每天加工吉祥物的个数相等且保持不变,由于生产需要,其中一个车间推迟两天开始加工,刚开始加工时,甲车间有10名工人,乙车间有12名工人,图中线段OB和折线ACB分别表示两个车间的加工情况.依据图中提供的信息,完成下列各题:
(1)线段OB反映的是 车间的加工情况;
(2)开始加工后,甲车间加工多少天后,两车间加工吉祥物数相同?
(3)根据折线段反映的加工情况,请你提出一个问题,并给出解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2012年6月3号国际田联钻石联赛美国尤金站比赛中,百米跨栏飞人刘翔以12.87s的成绩打破世界记录并轻松夺冠.A、B两镜头同时拍下了刘翔冲刺时的画面(如图),从镜头B观测到刘翔的仰角为60°,从镜头A观测到刘翔的仰角为30°,若冲刺时的身高大约为1.88m,请计算A、B两镜头之间的距离为 . (结果保留两位小数, ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
![]()
(1)当AC=10,BC=8时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=30°,则∠BOE=_______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为___________;
(2)当射线OE绕点O逆时针旋转到图2的位置时,(1)中∠BOE和∠COF的数量关系是否仍成立?请说明理由.
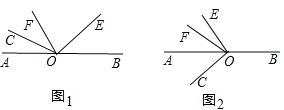
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.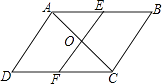
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人先后从公园大门出发,沿绿道向码头步行,乙先到码头并在原地等甲到达.图1是他们行走的路程y(m)与甲出发的时间x(min)之间的函数图象.
(1)求线段AC对应的函数表达式;
(2)写出点B的坐标和它的实际意义;
(3)设d(m)表示甲、乙之间的距离,在图2中画出d与x之间的函数图象(标注必要数据).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com