
【题目】如图,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 在
在![]() 的延长线上.
的延长线上.

(1)找出图中一对全等三角形,并证明其全等;
(2)求![]() 的度数?若
的度数?若![]() ,
,![]() ,求
,求![]() 的长。
的长。
【答案】(1)△ABD≌△ACE,证明见解析;(2)60°,5
【解析】
(1)根据等边三角形的性质推出AB=AC,AD=AE,∠BAC=∠DAE=60°,根据SAS可证△ABD≌△ACE;
(2)根据全等三角形的性质推出∠ABD=∠ACE,根据∠BAC+∠ABD=∠ACE+∠BEC,推出∠BEC=∠BAC=60°即可.
(1)△ABD≌△ACE,证明如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE, ∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△ABD≌△ACE.
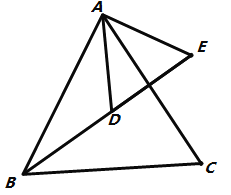
(2)如图,设AC与BE交于点O,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠EOC, ∠AOB+∠ABE+∠BAC=∠EOC+∠ACE+∠BEC,
∴∠BEC=∠BAC=60°,
即∠BEC =60°;
∵△ABD≌△ACE,
∴BD=CE=3,
∵△ADE是等边三角形,
∴DE=AE=2,
∴BE=BD+DE=3+2=5


科目:初中数学 来源: 题型:
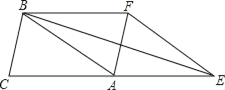
【题目】如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是![]() 的平分线上一点,若
的平分线上一点,若![]() ,求证:
,求证:![]() 为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,
为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,![]() ,AB=BC,
,AB=BC,![]() (下面请你连接AN,完成余下的证明过程)
(下面请你连接AN,完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是![]() 的平分线上一点,则当
的平分线上一点,则当![]() 时,试探究
时,试探究![]() 是何种特殊三角形,并证明探究结论.
是何种特殊三角形,并证明探究结论.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形
边形![]() ,试猜想:当
,试猜想:当![]() 的大小为多少时,(1)中的结论仍然成立?
的大小为多少时,(1)中的结论仍然成立?
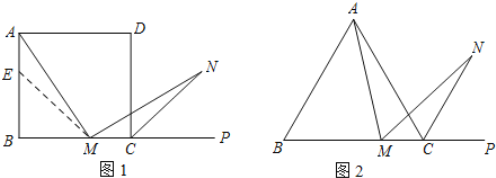
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时开始移动,点
同时开始移动,点![]() 的速度为
的速度为![]() 秒,点
秒,点![]() 的速度为
的速度为![]() 秒,点
秒,点![]() 移动到点
移动到点![]() 后停止,点
后停止,点![]() 也随之停止运动.下列时间瞬间中,能使
也随之停止运动.下列时间瞬间中,能使![]() 的面积为
的面积为![]() 的是( )
的是( )
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示.
(1)分别写出下列顶点的坐标:A_______,B______.
(2)顶点A关于y轴对称的点A′的坐标为:A′_______.
(3)△ABC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角△ABC中,∠C=90°,∠A=30°,AB=4,以AC为腰,在△ABC外作顶角为30°的等腰三角形ACD,连接BD.请画出图形,并直接写出△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.

(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com