
【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

【答案】(1)50、10、0.16;(2)144°;(3)![]() .
.
【解析】
(1)由B观点的人数和所占的频率即可求出总人数;由总人数即可求出a、b的值,
(2)用360°乘以D观点的频率即可得;
(3)画出树状图,然后根据概率公式列式计算即可得解
(1)参加本次讨论的学生共有12÷0.24=50,
则a=50×0.2=10,b=8÷50=0.16,
故答案为:50、10、0.16;
(2)D所在扇形的圆心角的度数为360°×0.4=144°;
(3)根据题意画出树状图如下:

由树形图可知:共有12中可能情况,选中观点D(合理竞争,合作双赢)的概率有6种,
所以选中观点D(合理竞争,合作双赢)的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市.张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施.已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①三点确定一个圆;②平分弦的直径必垂直于这条弦;③圆周角等于圆心角的一半;④等弧所对的圆心角相等;⑤各角相等的圆内接多边形是正多边形.其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
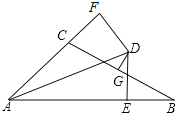
【题目】已知∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)连接CD、BD,求证:△CDF≌△BDE;
(2)若AE=5,AC=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是![]() 的平分线上一点,若
的平分线上一点,若![]() ,求证:
,求证:![]() 为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,
为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,![]() ,AB=BC,
,AB=BC,![]() (下面请你连接AN,完成余下的证明过程)
(下面请你连接AN,完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是![]() 的平分线上一点,则当
的平分线上一点,则当![]() 时,试探究
时,试探究![]() 是何种特殊三角形,并证明探究结论.
是何种特殊三角形,并证明探究结论.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形
边形![]() ,试猜想:当
,试猜想:当![]() 的大小为多少时,(1)中的结论仍然成立?
的大小为多少时,(1)中的结论仍然成立?
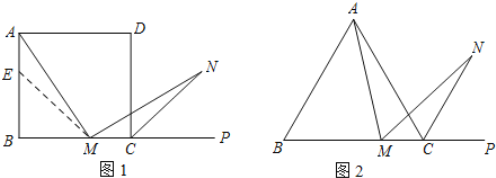
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示.
(1)分别写出下列顶点的坐标:A_______,B______.
(2)顶点A关于y轴对称的点A′的坐标为:A′_______.
(3)△ABC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、A、F三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
己知:______________________________________________________.
求证:______________________________________________________.
证明:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com