
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
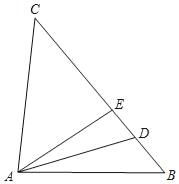
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
【答案】(1)证明见解析(2)48°
【解析】
(1)根据等腰三角形的性质得到∠CAD=∠CDA,根据角平分线的定义得到∠EAD=∠BAD,于是得到结论;
(2)设∠DAB=x,得到∠C=3x,根据角平分线的定义得到∠EAB=2∠DAB=2x,求得∠CAB=∠CAE+∠EAB=50°+2x,根据三角形的内角和即可得到结论.
(1)∵CA=CD,
∴∠CAD=∠CDA,
∵AD平分∠BAE,
∴∠EAD=∠BAD,
∵∠B=∠CDA﹣∠BAD,∠CAE=∠CAD﹣∠DAE,
∴∠CAE=∠B;
(2)设∠DAB=x,
∵∠C=∠3∠DAB,
∴∠C=3x,
∵∠CAE=∠B,∠B=50°,
∴∠CAE=50°,
∵AD平分∠BAE,
∴∠EAB=2∠DAB=2x,
∴∠CAB=∠CAE+∠EAB=50°+2x,
∵∠CAB+∠B+∠C=180°,
∴50°+2x+50°+3x=180°,
∴x=16°,
∴∠C=3×16°=48°.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分![]() ,BN
,BN![]() AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
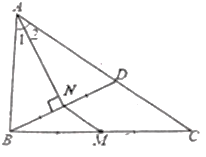
(1)求证:BN=DN;
(2)求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.
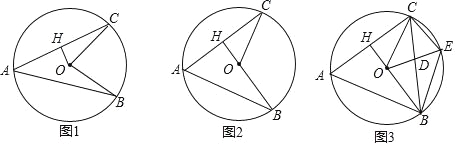
(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
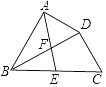
A. ![]()
![]() B.
B. ![]()
![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com