
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.
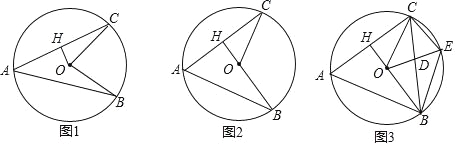
(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
【答案】(1)证明见解析.(2)∠BAC=60°;
(3)BM=5![]() ,
,![]() =
=![]() .
.
【解析】
试题分析:(1)如图1中,连接OA.欲证明∠B=∠C,只要证明△AOC≌△AOB即可.
(2)由OH⊥AC,推出AH=CH,由H、O、B在一条直线上,推出BH垂直平分AC,推出AB=BC,由AB=AC,推出AB=AC=BC,推出△ABC为等边三角形,即可解决问题.
(3)过点B作BM⊥CE延长线于M,过E、O作EN⊥BC于N,OK⊥BC于K.设ME=x,则BE=2x,BM=![]() x,在△BCM中,根据BC2=BM2+CM2,可得BM=5
x,在△BCM中,根据BC2=BM2+CM2,可得BM=5![]() ,推出sin∠BCM=
,推出sin∠BCM=![]() =
=![]() ,推出NE=
,推出NE=![]() ,OK=
,OK=![]() CK=
CK=![]() ,由NE∥OK,推出DE:OD=NE:OK即可解决问题.
,由NE∥OK,推出DE:OD=NE:OK即可解决问题.
试题解析:(1)如图1中,连接OA.

∵AB=AC,
∴弧AC=弧AB,
∴∠AOC=∠AOB,
在△AOC和△AOB中,
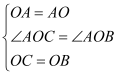 ,
,
∴△AOC≌△AOB,
∴∠B=∠C.
解:(2)连接BC,
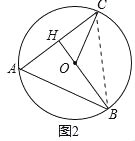
∵OH⊥AC,
∴AH=CH,
∵H、O、B在一条直线上,
∴BH垂直平分AC,
∴AB=BC,∵AB=AC,
∴AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.
解:(3)过点B作BM⊥CE延长线于M,过E、O作EN⊥BC于N,OK⊥BC于K.
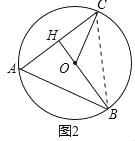
∵CH=7,
∴BC=AC=14,
设ME=x,
∵∠CEB=120°,
∴∠BEM=60°,
∴BE=2x,
∴BM=![]() x,
x,
△BCM中,∵BC2=BM2+CM2,
∴142=(![]() x)2+(6+x)2,
x)2+(6+x)2,
∴x=5或﹣8(舍弃),
∴BM=5![]() ,
,
∴sin∠BCM=![]() =
=![]() ,
,
∴NE=![]() ,
,
∴OK=![]() CK=
CK=![]() ,
,
∵NE∥OK,
∴DE:OD=NE:OK=45:49.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=
x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=![]() x+3上,若N点在第二象限内,则tan∠AON的值为( )
x+3上,若N点在第二象限内,则tan∠AON的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
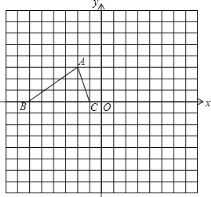
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.
(1)若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.
(2)在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
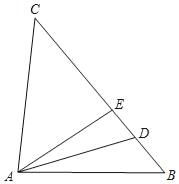
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 的中点,分别以
的中点,分别以![]() 为边作等腰
为边作等腰![]() 和等腰
和等腰![]() ,
,![]() ,连接
,连接![]() ,且
,且![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则下列说法中,不正确的是( )
,则下列说法中,不正确的是( )

A.![]() 是
是![]() 的中线B.四边形
的中线B.四边形![]() 是平行四边形
是平行四边形
C.![]() D.
D.![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
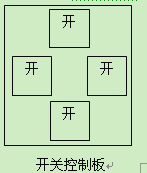
【题目】某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两
盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开
关与电灯、电扇的对应关系未知.
(1)若四个开关均正常,则任意按下一个开关,正好一盏灯亮的概率是多少?
(2)若其中一个控制电灯的开关坏了,则任意按下两个开关,正好一盏灯亮和一个扇转的概率是多少?请用树状图法或列表法加以说明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金80元,另外再按租车时间计费.
共享汽车:无固定租金,直接以租车时间(时)计费.
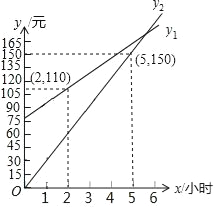
如图是两种租车方式所需费用y1(元)、y2(元)与租车时间x(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出y1、y2与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com