
【题目】某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.
(1)若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.
(2)在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?
【答案】(1)有2种进货方案:方案一:是购进甲种型号的电视机49台,乙种型号的电视机1台;方案二:是甲种型号的电视机50台,乙种型号的电视机0台;(2)方案一的利润大,最多为7550元.
【解析】
(1)设购进甲种型号的电视机x台,则乙种型号的电视机y台.数量关系为:两种不同型号的电视机50台,金额不超过76000元;
(2)根据利润=数量×(售价-进价),列出式子进行计算,即可得到答案.
解:(1)设购进甲种型号的电视机x台,则乙种型号的电视机(50-x)台.则
1500x+2100(50-x)≤76000,
解得:x≥48![]() .
.
则50≥x≥48![]() .
.
∵x是整数,
∴x=49或x=50.
故有2种进货方案:
方案一:是购进甲种型号的电视机49台,乙种型号的电视机1台;
方案二:是甲种型号的电视机50台,乙种型号的电视机0台;
(2)方案一的利润为:49×(1650-1500)+(2300-2100)=7550(元)
方案二的利润为:50×(1650-1500)=7500(元).
∵7550>7500
∴方案一的利润大,最多为7550元.


科目:初中数学 来源: 题型:
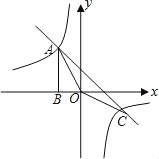
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 的边
的边![]() 在直线l上,
在直线l上,![]() ,且
,且![]() ,
,![]() 的边
的边![]() 也在直线上,边
也在直线上,边![]() 和边
和边![]() 重合,且
重合,且![]() .
.
(1)图①中,请你通过观察、测量、猜想,直接写出![]() 和
和![]() 的数量关系和位置关系;
的数量关系和位置关系;
(2)将![]() 沿直线l向右平移得到图②的位置时,
沿直线l向右平移得到图②的位置时,![]() 交
交![]() 于点D,连接
于点D,连接![]() ,
,![]() ,
,
求证:①![]() ;②
;②![]() ;
;
(3)将![]() 沿直线l向右平移得到图③的位置时,延长
沿直线l向右平移得到图③的位置时,延长![]() 交
交![]() 的延长线于点D,连接
的延长线于点D,连接![]() ,
,![]() ,你认为
,你认为![]() ,
,![]() 还成立吗?若成立,给予证明;若不成立,说明理由.
还成立吗?若成立,给予证明;若不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
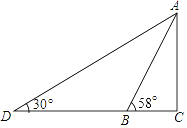
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.
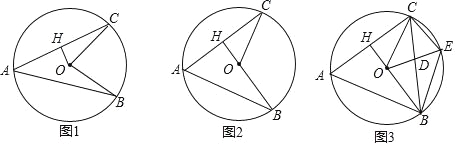
(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
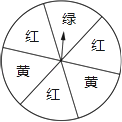
【题目】有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
查看答案和解析>>
科目:初中数学 来源: 题型:
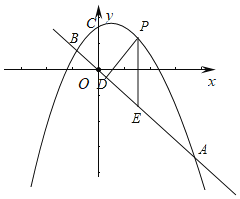
【题目】如图,已知抛物线y=-x2+bx+c与直线y=-x的交点A、B的横坐标分别为2和![]() .点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
.点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
(1)直接写出点A、B的坐标;
(2)求抛物线的关系式;
(3)判断△OBC形状,并说明理由;
(4)设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;
(5)定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com