
【题目】如图![]() 的边
的边![]() 在直线l上,
在直线l上,![]() ,且
,且![]() ,
,![]() 的边
的边![]() 也在直线上,边
也在直线上,边![]() 和边
和边![]() 重合,且
重合,且![]() .
.
(1)图①中,请你通过观察、测量、猜想,直接写出![]() 和
和![]() 的数量关系和位置关系;
的数量关系和位置关系;
(2)将![]() 沿直线l向右平移得到图②的位置时,
沿直线l向右平移得到图②的位置时,![]() 交
交![]() 于点D,连接
于点D,连接![]() ,
,![]() ,
,
求证:①![]() ;②
;②![]() ;
;
(3)将![]() 沿直线l向右平移得到图③的位置时,延长
沿直线l向右平移得到图③的位置时,延长![]() 交
交![]() 的延长线于点D,连接
的延长线于点D,连接![]() ,
,![]() ,你认为
,你认为![]() ,
,![]() 还成立吗?若成立,给予证明;若不成立,说明理由.
还成立吗?若成立,给予证明;若不成立,说明理由.

【答案】(1)![]() ,
,![]() ;(2)①证明见解析;②证明见解析;(3)成立,理由见解析.
;(2)①证明见解析;②证明见解析;(3)成立,理由见解析.
【解析】
(1)先证明△ABC为等腰直角三角形,再得出△ABC≌△EFP,从而根可以得出结论;
(2)①先判断出BF=DF,进而得出△BEF≌△DPF,即可得出结论;②连接![]() 并延长交
并延长交![]() 于M,根据①中全等可得
于M,根据①中全等可得![]() ,再证明∠EMP=90°即可得出结论;
,再证明∠EMP=90°即可得出结论;
(3)类比(2)的证明就可以得到,结论仍成立.
(1)解:![]() ,
,![]() .
.
证明如下:![]() 且
且![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
易知,![]() ≌
≌![]() ,
,
同理可证![]() ,
,
![]() ,
,
![]() 且
且![]() ;
;
(2)证明:①![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
![]() .
.
![]() 在
在![]() 和
和![]() 中,
中,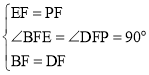 ,
,
![]() ≌
≌![]() ,
,
![]() .
.
②如图②,连接![]() 并延长交
并延长交![]() 于M,
于M,

![]() ≌
≌![]() ,
,
![]() .
.
![]() 在
在![]() 中,
中,![]() ,又
,又![]() ,
,
![]() .
.
![]() .
.
![]() ;
;
(3)解:成立.![]() ,
,![]() .
.
理由如下:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
![]() .
.
![]() 在
在![]() 和
和![]() 中,
中,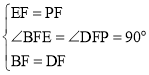 ,
,
![]() ≌
≌![]() ,
,
![]() .
.
如图③,延长![]() 交
交![]() 于N,
于N,
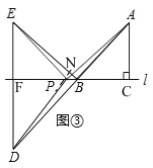
![]() ≌
≌![]() ,
,
![]() .
.
![]() 在
在![]() 中,
中,![]() ,又
,又![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
即:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
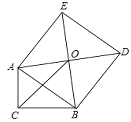
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
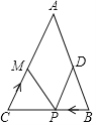
【题目】如图,![]() ,
,![]() ,点D为
,点D为![]() 的中点,点P在边
的中点,点P在边![]() 上以每秒
上以每秒![]() 的速度由点B向点C运动,同时,点M在边
的速度由点B向点C运动,同时,点M在边![]() 上由点C向点A匀速运动.
上由点C向点A匀速运动.
(1)当点M的运动速度与点P的运动速度相同,经过1秒后,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点M的运动速度与点P的运动速度不相等,当点M的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
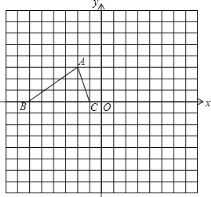
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.
(1)若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.
(2)在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 的中点,分别以
的中点,分别以![]() 为边作等腰
为边作等腰![]() 和等腰
和等腰![]() ,
,![]() ,连接
,连接![]() ,且
,且![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则下列说法中,不正确的是( )
,则下列说法中,不正确的是( )

A.![]() 是
是![]() 的中线B.四边形
的中线B.四边形![]() 是平行四边形
是平行四边形
C.![]() D.
D.![]() 平分
平分![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com