
【题目】2018年9月17日世界人工智能大会在.上海召开,人工智能的变革力在教育、制造等领域加速落地.在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一-部分.
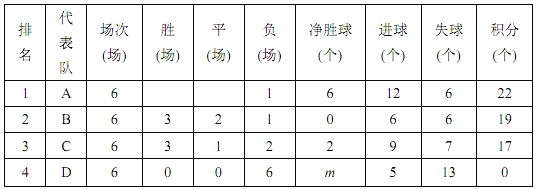
(说明:积分=胜场积分十平场积分+负场积分)
(1)D代表队的净胜球数m=______;
(2)本次决赛中,胜一场积______分,平一场积______分,负一场积_______分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下:如图,两侧最长斜拉索![]() ,
,![]() 相交于点
相交于点![]() ,分别与桥面交于
,分别与桥面交于![]() ,
,![]() 两点,且点
两点,且点![]() ,
,![]() ,
,![]() 在同一竖直平面内.测得
在同一竖直平面内.测得![]() ,
,![]() ,
,![]() 米,请帮助该小组根据测量数据,求斜拉索顶端点
米,请帮助该小组根据测量数据,求斜拉索顶端点![]() 到
到![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社的一则广告如下:

甲公司想分批组织员工到延安红色旅游学习.
(1)如果第一批组织40人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]()
![]() 经过点
经过点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .
.
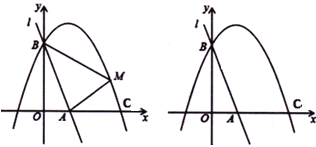
(1)求该抛物线的函数表达式;
(2)已知点![]() 是抛物线上的一个动点,并且点
是抛物线上的一个动点,并且点![]() 在第一象限内,连接
在第一象限内,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数表达式,并求出
的函数表达式,并求出![]() 的最大值及此时动点
的最大值及此时动点![]() 的坐标;
的坐标;
(3)将点![]() 绕原点旋转得点
绕原点旋转得点![]() ,连接
,连接![]() 、
、![]() ,在旋转过程中,一动点
,在旋转过程中,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位长度的速度运动到
个单位长度的速度运动到![]() 后停止,求点
后停止,求点![]() 在整个运动过程中用时最少是多少?
在整个运动过程中用时最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1),P2(x2,y2),如果![]() ,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
(1)在点D(-2,-2),E(5,-1),F(0,4)中,原点O的“4-距点"是____(填字母);
(2)已知点A(2,1),点B(0,b),过点B作平行于x轴的直线l.
①当b=3时,直线l上点A的“2-距点"的坐标为_______;
②若直线l上存在点A的2-距点”,求b的取值范围:
(3)已知点M(1,2),N(3,2),C(m,0),⊙C的半径为![]() ,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生身体发育状况,学校抽取一部分学生测量身高(单位:m),绘制处如下的统计图①和图②.请根据相关信息,解答下列问题:
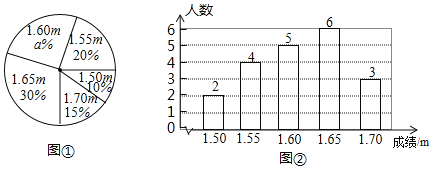
(1)图①中a的值为 ;
(2)求统计的这组学生身高数据的平均数、众数和中位数;
(3)如果全校七年级学生有300人,那么估计身高大于1.65m的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
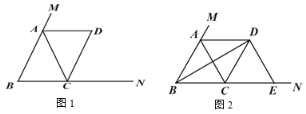
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com