
【题目】某旅行社的一则广告如下:

甲公司想分批组织员工到延安红色旅游学习.
(1)如果第一批组织40人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
【答案】(1)28000;(2)45人
【解析】
(1)首先表示出40人是平均每人的费用,进而得出总费用;
(2)表示出每人平均费用为:800﹣10(x﹣30),进而得出等式求出答案.
解:(1)∵人数多于30人,那么每增加1人,人均收费降低10元,
∴第一批组织40人去学习,则公司应向旅行社交费:40×[800﹣(40﹣30)×10]=28000(元);
故答案为:28000;
(2)设这次旅游应安排x人参加,
∵30×800=24000<29250,
∴x>30,根据题意得:
x[800﹣10(x﹣30)]=29250,
整理得,x2﹣110x+2925=0,
解得:x1=45,x2=65
∵800﹣10(x﹣30)≥500,
∴x≤60.
∴x=45.
答:这次旅游应安排45人参加.


科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点![]() ,
,![]() ,
,![]() .
.
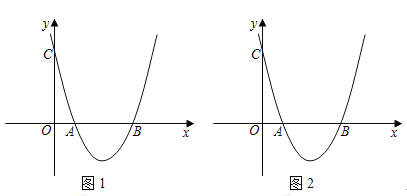
(1)求抛物线的解析式和对称轴;
(2)![]() 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足![]() 的值为最小的点
的值为最小的点![]() 坐标(请在图1中探索);
坐标(请在图1中探索);
(3)在第四象限的抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是以
是以![]() 为对角线且面积为
为对角线且面积为![]() 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点![]() 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是_______.
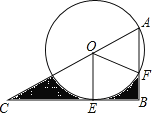
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有20名工人,每人每天加工甲种零件5个或乙种零件4个.在这20名工人当中,派x人加工甲种零件,其余的加工乙种零件,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可以获利24元.
(1)写出此工厂每天所获利润y(元)与x(人)之间的函数关系式(只写出解析式)
(2)若要使工厂每天获利不低于1800元,问至少要派多少人加工乙种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC、BD相交于点O,且AO=CO,AB∥CD.
(1)求证:AB=CD;
(2)若∠OAB=∠OBA,求证:四边形ABCD是矩形.
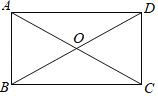
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月17日世界人工智能大会在.上海召开,人工智能的变革力在教育、制造等领域加速落地.在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一-部分.
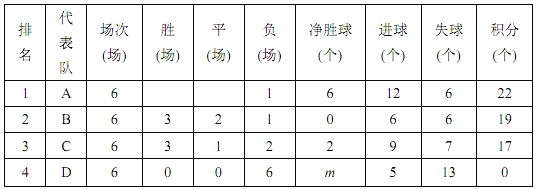
(说明:积分=胜场积分十平场积分+负场积分)
(1)D代表队的净胜球数m=______;
(2)本次决赛中,胜一场积______分,平一场积______分,负一场积_______分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com