
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
【答案】(1) B的坐标为(0,2) (2) (8,1)或(-8,-1)
【解析】试题分析:(1)根据双曲线经过点A(2,4),代入可得m的值;
接下来根据直线y=x+b经过点A,代入点A的坐标可得b的值,从而可得与y轴的交点坐标;
(2)设△OBP的边OB边上的高为x,根据三角形的面积可得![]() |x|·OB=8,从而可得点P的横坐标;再代入反比例函数可得点P的纵坐标,从而可得点P的坐标.
|x|·OB=8,从而可得点P的横坐标;再代入反比例函数可得点P的纵坐标,从而可得点P的坐标.
解:(1)∵双曲线y=![]() 经过点A(2,4),∴m=8.
经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),∴b=2.
∴此直线与y轴的交点B的坐标为(0,2).
(2) 设△OBP的边OB边上的高为x,则![]() |x|·OB=8,
|x|·OB=8,
∵交点B的坐标是(0,2),
∴OB=2,
解得x=±8,
∵点P在双曲线上,
∴y=±1,
∴点P的坐标是(8,1)或(-8,-1).
点P的坐标为(8,1)或(-8,-1).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某校八年级甲,乙两班各有![]() 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取
名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取![]() 名学生进行身体素质测试,测试成绩如下:
名学生进行身体素质测试,测试成绩如下:
甲班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
乙班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面数据,得到如下统计表:

样本数据的平均数、众数.中位数如下表所示:
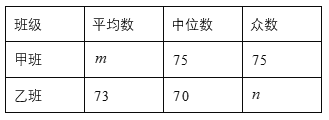
根据以上信息,解答下列问题:
(1)求表中![]() 的值
的值
(2)表中![]() 的值为( )
的值为( )
(3)若规定测试成绩在![]() 分以上(含
分以上(含![]() 分)的学生身体素质为优秀,请估计乙班
分)的学生身体素质为优秀,请估计乙班![]() 名学生中身体素质为优秀的学生的人数.
名学生中身体素质为优秀的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD,AB=4,∠ADC=120o,连接对角线AC、BD交于点O,
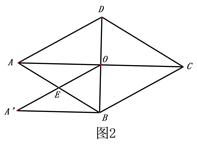
(1)如图2,将△AOD沿DB平移,使点D与点O重合,求平移后的△A′BO与菱形ABCD重合部分的面积.
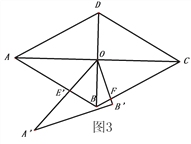
(2)如图3,将△A′BO绕点O逆时针旋转交AB于点E′,交BC于点F,
①求证:BE′+BF=2,
②求出四边形OE′BF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
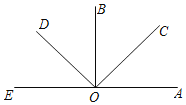
【题目】如图A、O、E三点在同一条直线上,∠AOB=∠COD=90°,观察图形后有以下四个结论,其中正确的结论是( )
A.∠BOC=∠AOC=∠BOD
B.图中小于平角的角有6个
C.∠BOC与∠AOD互补
D.∠BOD和∠AOC互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幻方”在中国古代称为“河图”、“洛书”,又叫“纵横图”.其主要性质是在一个由若干个排列整齐的数组成的正方形中,图中任意一横行,一纵行及对角线的几个数之和都相等.图(l)所示是一个![]() 幻方.有人建议向火星发射如图(2)所示的幻方图案,如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).图(3)是一个未完成的
幻方.有人建议向火星发射如图(2)所示的幻方图案,如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).图(3)是一个未完成的![]() 幻方,请你类比图(l)推算图(3)中
幻方,请你类比图(l)推算图(3)中![]() 处所对应的数字是( )
处所对应的数字是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=![]() 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).
(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=![]() 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管和一个出水管的容器,每分钟的进水量和出水量都是常数.从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水.如图表示的是容器中的水量y(升)与时间t(分钟)的图象.
(1)当4≤t≤12时,求y关于t的函数解析式;
(2)当t为何值时,y=27?
(3)求每分钟进水、出水各是多少升?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) | 5 | 6 | 8 | 9 | 10 |
射中此环的子弹数(发) | 4 | 1 | 3 | 1 | 1 |
乙
中靶环数(环) | 5 | 6 | 7 | 9 | 10 |
射中此环的子弹数(发) | 2 | 3 | 2 |
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com