
【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=![]() 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).
(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=![]() 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.

【答案】(1) y=![]() (2). y=x+7.
(2). y=x+7.
【解析】试题分析:(1)设反比例解析式为y=![]() ,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)设平移后的直线交y轴于H,根据两平行线间的距离相等,可得C到AB的距离与H到AB的距离相等,根据等底等高的三角形的面积相等,可得b的值,根据待定系数法,可得答案.
解:(1)∵点B(m,2)在直线y=x-2上,
∴m-2=2,解得m=4,∴点B(4,2).
又∵点B(4,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=8,∴反比例函数的关系式为y=![]() .
.
(2)设平移后的直线对应的函数关系式为y=x+b,C点坐标为![]() .
.
∵△ABC的面积为18,∴4×![]() -
-![]() ×4×4-
×4×4-![]() ×(4-x)
×(4-x)![]() -
-![]() x
x![]() =18,
=18,
化简,得x2+7x-8=0,解得x1=-8,x2=1.
∵x>0,∴x=1,∴C点坐标为(1,8).
把C点坐标(1,8)代入y=x+b得:8=1+b,∴b=7.
∴平移后的直线对应的函数关系式为y=x+7.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度![]() (千米/分钟)与时间
(千米/分钟)与时间![]() (分钟)的函数关系如图所示.
(分钟)的函数关系如图所示.

(1)当![]() 时,求
时,求![]() 关于
关于![]() 工的函数表达式,
工的函数表达式,
(2)求点![]() 的坐标.
的坐标.
(3)求高铁在![]() 时间段行驶的路程.
时间段行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点D是等腰Rt△ABC的斜边BC上一动点,连接AD,作等腰Rt△ADE,使AD=AE,且∠DAE=90°连接BE、CE.

(1)判断BD与CE的数量关系与位置关系,并进行证明;
(2)当四边形ADCE的周长最小值是6时,求BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线m:y=﹣2x2﹣2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
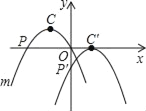
A. C(﹣![]() ,
,![]() ) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣
) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y1=k1x+2的图象与反比例函数y2=![]() 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.

(1)k1=__________,k2=__________;
(2)根据函数图象可知,当y1>y2时,x的取值范围是____________;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODACS△ODE=31时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40kg到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 1.2 | 1.5 |
零售价(单位:元/kg) | 2.0 | 2.8 |
问:他当天卖完这些西红柿和豆角能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
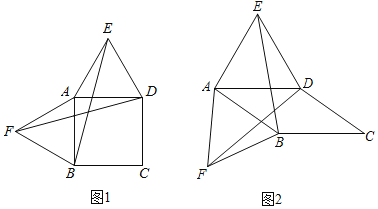
【题目】如图,以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接BE、DF.
(1)当四边形ABCD为正方形时(如图1),则线段BE与DF的数量关系是 .
(2)当四边形ABCD为平行四边形时(如图2),问(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,李敏发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:
S=1+3+32+33+34+35+36+37+38①
然后在①式的两边都乘3,得,
3S=3+32+33+34+35+36+37+38+39②
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S=![]()
请爱动脑筋的你求出1+5+52+53+54+…+52019的值.
正确答案是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com